题目内容
4. 如图,方格纸中每个小正方形的边长都是1,点A、B、C、D都在格点上,在△ABC中,∠ACB=90°,AC=BC.
如图,方格纸中每个小正方形的边长都是1,点A、B、C、D都在格点上,在△ABC中,∠ACB=90°,AC=BC.(1)将△CBD绕点C逆时针方向旋转,使点B旋转到点A的位置,画出旋转后的△CAD′;
(2)求点D旋转到D′时线段CD扫过的图形的面积.
分析 (1)由于∠ACB=90°,AC=BC,所以△CBD绕点C逆时旋转90°可得到△CAD′,于是利用网格特点和性质的性质画出点D的对应点D′即可;
(2)由于线段CD扫过的图形为扇形,此扇形是以C点为圆心,CD为半径,圆心角为90°的扇形,所以利用扇形面积公式计算即可.
解答 解:(1)如图,△CAD′为所作;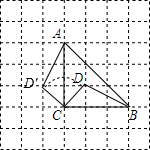
(2)CD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
线段CD扫过的图形的面积=$\frac{90•π•(\sqrt{2})^{2}}{360}$=$\frac{1}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了扇形面积公式.

练习册系列答案
相关题目
9.在比例尺是1:46000的城市交通游览图上,某条道路的图上距离长约8cm,则这条道路的实际长度约为( )
| A. | 368×103cm | B. | 36.8×104cm | C. | 3.68×105cm | D. | 3.68×106cm |
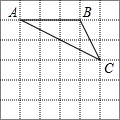 在如图所示的方格纸中,每个小正方形的边长都为1,点A、B、C均为格点(每个小正方形的顶点称为格点).
在如图所示的方格纸中,每个小正方形的边长都为1,点A、B、C均为格点(每个小正方形的顶点称为格点). 如图,一副直角三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC,∠MON的度数为45°.
如图,一副直角三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC,∠MON的度数为45°. 如图:AOB为直线,OC平分∠AOD,∠BOD=42°,则∠AOC=69°.
如图:AOB为直线,OC平分∠AOD,∠BOD=42°,则∠AOC=69°. 如图,已知∠1=∠2,∠A=∠F,试说明:∠C=∠D.请补充说明过程,并在括号内填上相应理由.
如图,已知∠1=∠2,∠A=∠F,试说明:∠C=∠D.请补充说明过程,并在括号内填上相应理由. 如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).