题目内容
若x2+ax=(x+
)2+b,则a、b的值分别是 .
| 1 |
| 2 |
考点:配方法的应用
专题:
分析:首先整理得出ax=x+b+
,得出a=1,则b+
=0,得出b=-
,由此解决问题.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:∵x2+ax=(x+
)2+b,
∴ax=x+b+
,
∴a=1,b+
=0,解得b=-
.
故答案为:a=1,b=-
.
| 1 |
| 2 |
∴ax=x+b+
| 1 |
| 4 |
∴a=1,b+
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:a=1,b=-
| 1 |
| 4 |
点评:此题考查整式的混合运算,注意字母与常数项的对应关系是解决问题的关键.

练习册系列答案
相关题目
已知正比例函数y1=k1x和反比例函数y2=
的图象都经过点(1,2),则k1、k2的值分别为( )
| k2 |
| x |
A、k1=2,k2=
| ||||
B、k1=
| ||||
| C、k1=2,k2=2 | ||||
D、k1=
|
 操作探究:
操作探究: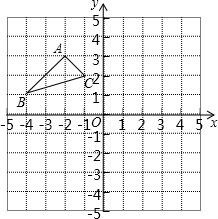 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.