题目内容
13.在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
分析 (1)直接根据概率公式求解;
(2)画树状图展示所有12种等可能的结果数,再找出刚好是一男生一女生的结果数,然后根据概率公式求解.
解答 解:(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,刚好是男生的概率=$\frac{3}{3+4}$=$\frac{3}{7}$;
(2)画树状图为:
共有12种等可能的结果数,其中刚好是一男生一女生的结果数为6,
所以刚好是一男生一女生的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
3.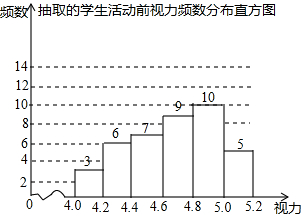 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.| 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
4.一元二次方程2x2-3x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8.不等式$\frac{x+1}{2}$>$\frac{2x+2}{3}$-1的正整数解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )| A. | 80° | B. | 85° | C. | 90° | D. | 95° |
9. 如图,A,B两点表示的数( )
如图,A,B两点表示的数( )
 如图,A,B两点表示的数( )
如图,A,B两点表示的数( )| A. | 互为倒数 | B. | 互为相反数 | C. | 都是有理数 | D. | 都是正数 |