题目内容
5.一般地,当α、β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α-β)=sinα•cosβ-cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×$\frac{1}{2}$=1.类似地,可以求得sin15°的值是$\frac{\sqrt{6}-\sqrt{2}}{4}$.分析 把15°化为60°-45°,则可利用sin(α-β)=sinα•cosβ-cosα•sinβ和特殊角的三角函数值计算出sin15°的值.
解答 解:sin15°=sin(60°-45°)=sin60°•cos45°-cos60°•sin45°=$\frac{\sqrt{3}}{2}$•$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$.
故答案为$\frac{\sqrt{6}-\sqrt{2}}{4}$.
点评 本题考查了特殊角的三角函数值:应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.也考查了阅读理解能力.

练习册系列答案
相关题目
15.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20. 如图,一个空心圆柱体,其主视图正确的是( )
如图,一个空心圆柱体,其主视图正确的是( )
 如图,一个空心圆柱体,其主视图正确的是( )
如图,一个空心圆柱体,其主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
10.反比例函数y=$\frac{1-6t}{x}$的图象与直线y=-x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
| A. | t<$\frac{1}{6}$ | B. | t>$\frac{1}{6}$ | C. | t≤$\frac{1}{6}$ | D. | t≥$\frac{1}{6}$ |
17.将5570000用科学记数法表示正确的是( )
| A. | 5.57×105 | B. | 5.57×106 | C. | 5.57×107 | D. | 5.57×108 |
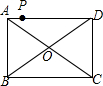 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )