题目内容
5.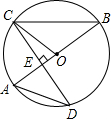 如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4$\sqrt{2}$,AE=2,求圆O的半径.
分析 (1)首先求出∠ADE的度数,再根据圆周角定理求出∠AOC的度数,最后求出∠OCE的度数;
(2)由弦CD与直径AB垂直,利用垂径定理得到E为CD的中点,求出CE的长,在直角三角形OCE中,设圆的半径OC=r,OE=OA-AE,表示出OE,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径r的值.
解答 解:(1)∵CD⊥AB,∠A=48°,
∴∠ADE=42°.
∴∠AOC=2∠ADE=84°,
∴∠OCE=90°-84°=6°;
(2)解:因为AB是圆O的直径,且CD⊥AB于点E,所以CE=$\frac{1}{2}$CE=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,
在Rt△OCE中,OC2=CE2+OE2,
设圆O的半径为r,则OC=r,OE=OA-AE=r-2,所以r2=(2$\sqrt{2}$)2+(r-2)2,
解得:r=3.所以圆O的半径为3.
点评 此题考查了垂径定理,勾股定理,以及圆周角定理,熟练掌握定理是解本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
16.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{3x-2y=m+8}\\{2x-3y=m}\end{array}\right.$ 的解适合x-y=4,则m的值( )
| A. | 14 | B. | -14 | C. | 6 | D. | -6 |
20.由二次函数y=2(x-3)2+1可知( )
| A. | 其图象的开口向下 | B. | 其图象的对称轴为x=-3 | ||
| C. | 其最大值为1 | D. | 当x<3时,y随x的增大而减小 |
10.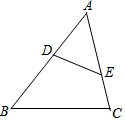 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{BC}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
17.将抛物线y=x2向上平移2个单位,再向右平移1个单位,那么所得新抛物线的表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-2)2+1 | D. | y=(x+2)2+1 |
15.数据1、2、3、4、5,这组数据的极差是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

 如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,AC=8cm,AE=4cm,则DE的长是3cm.
如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,AC=8cm,AE=4cm,则DE的长是3cm.