题目内容
19.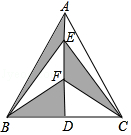 如图,在等边三角形ABC中,AD是BC边上的高,点E、F是AD上的 两点,AB=8cm,AD=4$\sqrt{3}$cm,则图中阴影部分的面积是8$\sqrt{3}$cm.
如图,在等边三角形ABC中,AD是BC边上的高,点E、F是AD上的 两点,AB=8cm,AD=4$\sqrt{3}$cm,则图中阴影部分的面积是8$\sqrt{3}$cm.
分析 根据等边三角形性质求出BD=DC,AD⊥BC,推出△CEF和△BEF关于直线AD对称,得出S△BEF=S△CEF,根据图中阴影部分的面积是$\frac{1}{2}$S△ABC求出即可.
解答 解:∵AB=AC,BC=4,AD是△ABC的中线,
∴BD=DC=$\frac{1}{2}$BC=4,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×8×4$\sqrt{3}$=16$\sqrt{3}$,
∴图中阴影部分的面积是$\frac{1}{2}$S△ABC=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$
点评 本题考查了勾股定理、轴对称的性质.通过观察可以发现是轴对称图形,且阴影部分的面积为全面积的一半,根据轴对称图形的性质求解.其中看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.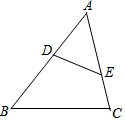 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{BC}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
7.下列命题是假命题的是( )
| A. | 有一个角为60°的等腰三角形是等边三角形 | |
| B. | 等角的补角相等 | |
| C. | 锐角三角形每个角都小于90° | |
| D. | 内错角相等 |
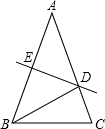 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于D,交AB于E,若△ABC的周长为22,BC=6,则△BCD的周长为14.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于D,交AB于E,若△ABC的周长为22,BC=6,则△BCD的周长为14.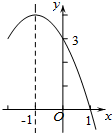 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.