题目内容
2．二次函数y=ax2+bx+c（a≠0）图象上部分点的坐标（x，y）对应值列表如表：| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
分析 关于对称轴对称的点其函数值相等，据此可确定出对称点，可求得其对称轴．
解答 解：
∵当x=-3和x=-1时，y=-3，
∴点（-3，-3）和点（-1，-3）关于对称轴对称，
∴对称轴为x=$\frac{-3+（-1）}{2}$=-2，
故答案为：直线x=-2．
点评 本题主要考查二次函数的性质，掌握二次函数的对称性是解题的关键．
练习册系列答案
星级口算天天练系列答案
相关题目
将正整数按如图所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示实数9．寻找规律，然后解答：
如图，在△ABC中，∠C=90°，BD是∠ABC的平分线，DE⊥AB，AC=8cm，AE=4cm，则DE的长是3cm．
10．
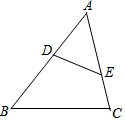已知，如图，在△ABC中，∠ADE=∠C，则下列等式成立的是（ ）
已知，如图，在△ABC中，∠ADE=∠C，则下列等式成立的是（ ）| A． | $\frac{AD}{AB}$=$\frac{AE}{BC}$ | B． | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C． | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D． | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
17．将抛物线y=x2向上平移2个单位，再向右平移1个单位，那么所得新抛物线的表达式是（ ）
| A． | y=（x-1）2+2 | B． | y=（x+1）2+2 | C． | y=（x-2）2+1 | D． | y=（x+2）2+1 |
7．下列命题是假命题的是（ ）
| A． | 有一个角为60°的等腰三角形是等边三角形 | |
| B． | 等角的补角相等 | |
| C． | 锐角三角形每个角都小于90° | |
| D． | 内错角相等 |
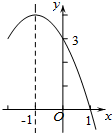二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，对称轴为直线x=-1，与x轴的一个交点为（1，0），与y轴的交点为（0，3），则方程ax2+bx+c=0（a≠0）的解为x1=1，x2=-3．