题目内容
简算:
×
×
×…
.
| 2 |
| 1+2 |
| 2+3 |
| 1+2+3 |
| 2+3+4 |
| 1+2+3+4 |
| 2+3+4+…+50 |
| 1+2+3+…+50 |
考点:有理数的混合运算
专题:
分析:先计算1+2+3+…n=
,而分子比分母少1,所以分子为
-1=
,所以
=
,则可表示出每一个分数,再进行约分即可.
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| (n+2)(n-1) |
| 2 |
| 2+3+4+…+n |
| 1+2+3+…+n |
| (n+2)(n-1) |
| n(n+1) |
解答:解:原式=
×
×
×
×
×…×
×
×
=
=
=
.
| 4×1 |
| 2×3 |
| 5×2 |
| 3×4 |
| 6×3 |
| 4×5 |
| 7×4 |
| 5×6 |
| 8×5 |
| 6×7 |
| 50×47 |
| 48×49 |
| 51×48 |
| 49×50 |
| 52×49 |
| 50×51 |
=
| (4×5×6×7×8×…×52)×(1×2×3×…×49) |
| (2×3×4×5×…×50)×(3×4×5×…×51) |
=
| 52 |
| 50×3 |
=
| 26 |
| 75 |
点评:本题主要考查有理数的计算,找出分母和分子的变化规律是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
一次课堂练习,小张做了如下4道因式分解题,你认为小张做得不够完整的一题是( )
| A、x2-y2=(x+y)(x-y) |
| B、x2y-xy2=xy(x-y) |
| C、1-4x2=(1+2x)(1-2x) |
| D、x3-x=x(x2-1) |
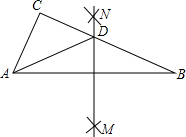 如图,在△ABC中,分别以点A和点B为圆心,大于
如图,在△ABC中,分别以点A和点B为圆心,大于 如图,将正方形ABCD绕B点旋转a(0°<a<90°),使A′D′交DC于E点.试猜想A′E与CE的数量关系,并证明你的结论.
如图,将正方形ABCD绕B点旋转a(0°<a<90°),使A′D′交DC于E点.试猜想A′E与CE的数量关系,并证明你的结论.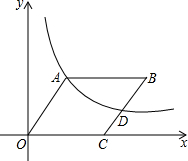 如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=
如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=