题目内容
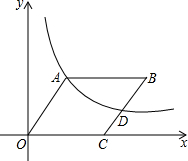 如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=
如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=| 2 |
| 3 |
| k |
| x |
(1)求反比例函数的解析式,并直接写出顶点B的坐标;
(2)猜想点D是否为BC的中点,并说明理由.
考点:反比例函数综合题
专题:
分析:(1)作AE⊥OC于点E,在直角△OAE中利用三角函数以及勾股定理求得OE和AE的长,即可求得A的坐标,利用待定系数即可求得反比例函数解析式,求得B的坐标;
(2)求得BC的中点坐标,代入反比例函数解析式即可判断.
(2)求得BC的中点坐标,代入反比例函数解析式即可判断.
解答: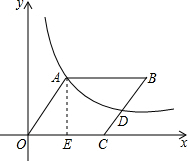 解:(1)作AE⊥OC于点E.
解:(1)作AE⊥OC于点E.
∵四边形OABC是菱形,
∴OA=OC=6,
又∵cos∠AOC=
=
,
∴OE=
OA=
×6=4,
在直角△OAE中,AE=
=
=2
,
则A的坐标是(4,2
),代入y=
,得:k=8
.
则反比例函数的解析式是:y=
.
B的坐标是(10,2
);
(2)BC的中点的坐标是(8,
).
把x=8,y=
代入y=
成立,
则BC的中点在反比例函数的图象上,即D是BC的中点.
 解:(1)作AE⊥OC于点E.
解:(1)作AE⊥OC于点E.∵四边形OABC是菱形,
∴OA=OC=6,
又∵cos∠AOC=
| OE |
| OA |
| 2 |
| 3 |
∴OE=
| 2 |
| 3 |
| 2 |
| 3 |
在直角△OAE中,AE=
| OA2-OE2 |
| 62-42 |
| 5 |
则A的坐标是(4,2
| 5 |
| k |
| x |
| 5 |
则反比例函数的解析式是:y=
8
| ||
| x |
B的坐标是(10,2
| 5 |
(2)BC的中点的坐标是(8,
| 5 |
把x=8,y=
| 5 |
8
| ||
| x |
则BC的中点在反比例函数的图象上,即D是BC的中点.
点评:本题考查了待定系数法求函数的解析式以及三角函数、菱形的性质,求得A的坐标是关键.

练习册系列答案
相关题目
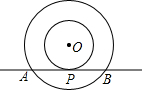 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,大圆、小圆的半径分别为10cm和6cm,则AB=
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,大圆、小圆的半径分别为10cm和6cm,则AB= 如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.