题目内容
14. 如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.
如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.
分析 连接DB于AC相交于M,根据已知和菱形的性质可分别求得AC,AE,AG的长,从而可发现规律根据规律不难求得第2015$\frac{1}{2}$个菱形的边长.
解答  解:连接DB,
解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM=$\frac{1}{2}$,
∴AM=$\frac{\sqrt{3}}{2}$,
∴AC=$\sqrt{3}$,
同理可得AE=$\sqrt{3}$AC=$(\sqrt{3})^{2}$,AG=$\sqrt{3}$AE=3$\sqrt{3}$=$(\sqrt{3})^{3}$,
按此规律所作的第n个菱形的边长为$(\sqrt{3})^{n-1}$,
则所作的第2015个菱形的边长是$(\sqrt{3})^{2015-1}=(\sqrt{3})^{2014}$.
故答案为:$(\sqrt{3})^{2014}$.
点评 此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力,解决本题的关键是发现规律.

练习册系列答案
相关题目
2.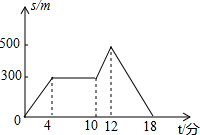 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
 星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的关系.依据图象,下面描述符合小红散步情景的是( )| A. | 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 | |
| B. | 从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 | |
| C. | 从家出发,一直散步(没有停留),然后回家了 | |
| D. | 从家出发,散了一会儿步,就找同学去了,18min后才开始返回 |
9.将△ABC的各顶点的横坐标分别加上3,纵坐标不变,连接所得三点组成的三角形是由△ABC( )
| A. | 自左平移3个单位长度得到的 | B. | 向右平移3个单位长度得到的 | ||
| C. | 向上平移3个单位长度得到的 | D. | 向下平移3个单位长度得到的 |
19.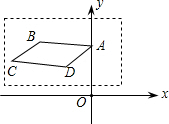 在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
 在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )
在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(4,-2)处,则此平移可以是( )| A. | 先向右平移5个单位,再向下平移1个单位 | |
| B. | 先向右平移5个单位,再向下平移3个单位 | |
| C. | 先向右平移4个单位,再向下平移4个单位 | |
| D. | 先向右平移4个单位,再向下平移3个单位 |
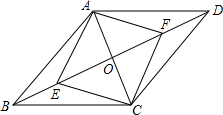 如图,在平行四边形ABCD中,AC、BD相交于点O,点E、F分别是OB、OD的中点.判断四边形AECF的形状并说明理由.
如图,在平行四边形ABCD中,AC、BD相交于点O,点E、F分别是OB、OD的中点.判断四边形AECF的形状并说明理由.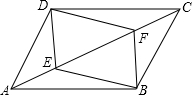 如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形. 如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )
如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( ) 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为(45,10).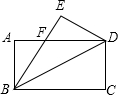 如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.