题目内容
19.先化简,再求代数式$\frac{3a+2b}{{a}^{2}-{b}^{2}}-\frac{2a+b}{{a}^{2}-{b}^{2}}$的值.其中:a=$\sqrt{2}$+1,b是正整数,且满足关于x的一元二次方程x2-4x+2b=0有两个不相等的实数根.分析 先根据分式混合运算的法则把原式进行化简,再根据关于x的一元二次方程x2-4x+2b=0有两个不相等的实数根求出b的值,在把a、b的值代入进行计算即可.
解答 解:原式=$\frac{3a+2b-2a-b}{{a}^{2}-{b}^{2}}$
=$\frac{a+b}{(a+b)(a-b)}$
=$\frac{1}{a-b}$,
∵关于x的一元二次方程x2-4x+2b=0有两个不相等的实数根,
∴△=(-4)2-4×1×2b>0,解得b<2.
∵b是正整数,
∴b=1,
∵a=$\sqrt{2}$+1,
∴原式=$\frac{1}{\sqrt{2}+1-1}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.下列代数运算正确的是( )
| A. | (x3)2=x5 | B. | (2x)2=2x2 | C. | (x+1)2=x2+1 | D. | x3•x2=x5 |
7.-5的相反数是( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | ±5 |
14.定义运算a?b=a(1-b),下面给出的关于这种运算的四个结论中正确的是( )
| A. | 2?(-2)=-4 | B. | a?b=b?a | C. | (-2)?2=2 | D. | 若a?b=0,则a=0 |
11.-$\frac{1}{3}$的相反数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -$\frac{1}{3}$ |
4.下列运算正确的是( )
| A. | (-2x2)3=-8x6 | B. | (a3)2=a5 | C. | a3•(-a)2=-a5 | D. | (-x)2÷x=-x |
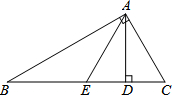 如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽△DBA,△BAD∽△ACD(写出一个三角形即可).
如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽△DBA,△BAD∽△ACD(写出一个三角形即可).