题目内容
9.已知 x=$\sqrt{5}+\sqrt{7}$,y=$\sqrt{5}-\sqrt{7}$,求下列代数式的值:(1)x2+y2
(2)$\frac{y}{x}+\frac{x}{y}$.
分析 先求得x+y=2$\sqrt{5}$,xy=-2,
(1)利用完全平方公式变形,将x+y与xy的值代入计算即可求出值;
(2)首先把所求的式子变形成$\frac{(x+y)^{2}}{xy}$-2的形式,然后代入数值计算即可求解.
解答 解:∵x=$\sqrt{5}+\sqrt{7}$,y=$\sqrt{5}-\sqrt{7}$,
∴x+y=2$\sqrt{5}$,xy=-2,
(1)x2+y2=(x+y) 2-2xy=(2$\sqrt{5}$)2-2×(-2)=24;
(2)$\frac{y}{x}+\frac{x}{y}$=$\frac{(x+y)^{2}}{xy}$-2=$\frac{20}{-2}$-2=-12.
点评 本题考查了二次根式的化简求值,正确对所求的式子进行变形是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
17.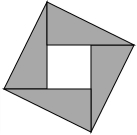 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
1.三元一次方程组$\left\{\begin{array}{l}a-b+c=0\\ 4a+2b+c=3\\ 2a+b-3c=19\end{array}\right.$消去一个未知数后,所得二元一次方程组是( )
| A. | $\left\{\begin{array}{l}a+b=1\\ 2a+b=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}3a+b=3\\ 2a+b=4\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}a+b=1\\ 3a-2c=19\end{array}\right.$ | D. | $\left\{\begin{array}{l}5a-2b=19\\ 3a+b=3\end{array}\right.$ |
19.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是( )
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐60°,第二次右拐60° | ||
| C. | 第一次左拐60°,第二次左拐120° | D. | 第一次右拐60°,第二次右拐60° |
 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.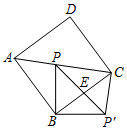 如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.
如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.