题目内容
4.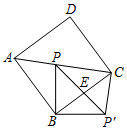 如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.
如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.(1)求证:△BAP≌△BCP′;
(2)探究:线段PA,PC,PB之间满足什么数量关系,请写出结论并证明;
(3)若PA<PC,当PB=5$\sqrt{2}$时,求BE的长.
分析 (1)证出∠ABP=∠CBP',由SAS证明△BAP≌△BCP′即可;
(2)由全等三角形的性质得出∠BAP=∠BCP′=45°,PA=P′C.证出∠PCP′=∠BCA+∠BCP′=90°.由勾股定理即可得出结论;
(3)设PA=x,则PC=14-x.由勾股定理得出方程,解方程求出PA,证明△CPE∽△ABP.得出对应边成比例求出EC,即可得出BE的长.
解答 (1)证明:∵线段BP绕点B顺时针旋转90°得到线段BP′,
∴BP=BP′,∠PBP′=90°.
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°.
∴∠ABC=∠PBP′.
∴∠ABC-∠PBC=∠PBP′-∠PBC,即∠ABP=∠CBP′.
在△BAP和△BCP′中,$\left\{\begin{array}{l}{BA=BC}&{\;}\\{∠ABP=∠CBP′}&{\;}\\{BP=BP′}&{\;}\end{array}\right.$,
∴△BAP≌△BCP′(SAS).
(2)解:结论:PA2+PC2=2PB2.
证明:∵四边形ABCD是正方形,
∴∠BAC=$\frac{1}{2}$∠BAD=45°,∠BCA=$\frac{1}{2}$∠BCD=45°.
由(1)知,△BAP≌△BCP′,
∴∠BAP=∠BCP′=45°,PA=P′C.
∴∠PCP′=∠BCA+∠BCP′=45°+45°=90°.
在Rt△PCP′中,由勾股定理,得P′C2+PC2=P′P2,
∴PA2+PC2=P′P2.
又在Rt△PBP′中,P′P2=PB2+P′B2=2PB2.
∴PA2+PC2=2PB2.
(3)解:∵∠ABC=90°,AB=BC=7$\sqrt{2}$,
∴AC=$\sqrt{2}$AB=14.
设PA=x,则PC=14-x.
又∵PB=5$\sqrt{2}$,
∴x2+(14-x)2=2(5$\sqrt{2}$)2,
解得x1=6,x2=8.
当x=6时,PA=6,PC=8,符合题意;
当x=8时,PA=8,PC=6,PA>PC,不符合题意.
∴PA=6,PC=8.
∵∠PBP′=90°,PB=P′B,
∴∠BPP′=45°.
∵∠BPC=∠BAP+∠ABP,
∴∠BPP′+∠CPE=∠BAP+∠ABP,即45°+∠CPE=45°+∠ABP.
∴∠CPE=∠ABP.
又∠PCE=∠BAP=45°,
∴△CPE∽△ABP.
∴$\frac{EC}{PA}=\frac{PC}{BA}$,即$\frac{EC}{6}=\frac{8}{7\sqrt{2}}$.
∴EC=$\frac{24\sqrt{2}}{7}$.
∴BE=BC-EC=7$\sqrt{2}$-$\frac{24\sqrt{2}}{7}$=$\frac{25\sqrt{2}}{7}$.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | $\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=-2}\\{y=-1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=2}\\{y=-1}\end{array}}\right.$ |
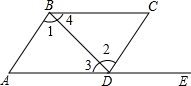 如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )
如图,E点是AD延长线上一点,下列条件中,不能判定直线AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠CDE | D. | ∠C+∠1+∠4=180° |
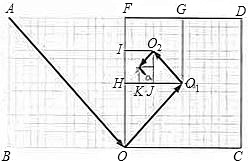 如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走2走到正方形O3KJP的中心O4,一共走了31$\sqrt{2}$m,则长方形花坛ABCD的周长是96m.
如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心O1,再从中心O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走2走到正方形O3KJP的中心O4,一共走了31$\sqrt{2}$m,则长方形花坛ABCD的周长是96m.