题目内容
15.感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB-AC=$\sqrt{2}$a(用含a的代数式表示)
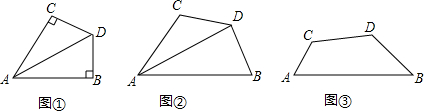
分析 探究:欲证明DB=DC,只要证明△DFC≌△DEB即可.
应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BD=$\sqrt{2}$EB即可解决问题.
解答 探究:
证明:如图②中,DE⊥AB于E,DF⊥AC于F,
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
$\left\{\begin{array}{l}{∠F=∠DEB}\\{∠FCD=∠B}\\{DF=DE}\end{array}\right.$,
∴△DFC≌△DEB,
∴DC=DB.
应用:解;如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
$\left\{\begin{array}{l}{∠F=∠DEB}\\{∠FCD=∠B}\\{DC=DB}\end{array}\right.$,
∴△DFC≌△DEB,
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴△ADF≌△ADE,
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在RT△DEB中,∵∠DEB=90°,∠B=∠EDB=45°,BD=a,
∴BE=$\frac{\sqrt{2}}{2}$a,
∴AB-AC=$\sqrt{2}$a.
故答案为$\sqrt{2}$a.
点评 本题考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.

| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
| A. | ±1 | B. | 1 | C. | 2 | D. | 9 |
| A. | 2.36×108 | B. | 2.36×109 | C. | 2.36×1010 | D. | 2.36×1011 |
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
 如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证: