题目内容
20. 如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
分析 (1)欲证明∠CEB=∠CBE,只要证明∠CEB=∠ABD,∠CBE=∠ABD即可.
(2)先证明四边形CEDB是平行四边形,再根据BC=BD即可判定.
解答 证明;(1)∵△ABC≌△ABD,
∴∠ABC=∠ABD,
∵CE∥BD,
∴∠CEB=∠DBE,
∴∠CEB=∠CBE.
(2))∵△ABC≌△ABD,
∴BC=BD,
∵∠CEB=∠CBE,
∴CE=CB,
∴CE=BD
∵CE∥BD,
∴四边形CEDB是平行四边形,
∵BC=BD,
∴四边形CEDB是菱形.
点评 本题考查全等三角形的性质、菱形的判定、平行四边形的判定等知识,熟练掌握全等三角形的性质是解题的关键,记住平行四边形、菱形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
10.下列各组数中互为相反数的是( )
| A. | 2 与-$\frac{1}{2}$ | B. | -2与2 | C. | 2 与丨-2| | D. | $\frac{1}{2}$与-2 |
12.运用乘法公式计算(m+2)(m-2)的结果是( )
| A. | m2-2 | B. | m2-4 | C. | m2+4 | D. | m2+2 |
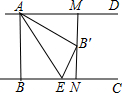 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为$\frac{3\sqrt{2}}{2}$或$\frac{3\sqrt{5}}{5}$.
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为$\frac{3\sqrt{2}}{2}$或$\frac{3\sqrt{5}}{5}$.