Question

11．我们把过三角形的一个顶点且能将这个三角形分割成两个等腰三角形的线段称为该三角形的“等腰线段”．
例如：Rt△ABC，取边AB的中点D，线段CD就是△ABC的等腰线段．
（1）请分别画出下列三角形的等腰线段；

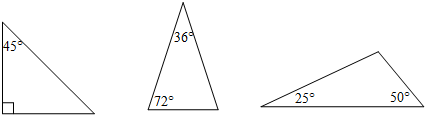
（2）如图，在△EFG中，若∠G=2∠F，且△EFG有等腰线段，请直接写出∠F的度数的取值范围．

Answer 1

分析 （1）利用三角形的等腰线段的定义画图；
（2）设∠F=x，则∠G=2x，讨论：如图2，线段EM是等腰线段，则EM=EG，ME=MF，所以∠F=∠MEF=x，∠EMG=∠G=2x，根据三角形内角和得到2x＜90°，则x＜45°；如图3，GN为等腰线段，
则NF=NG，GN=GE，所以∠F=∠NGF=x，∠E=∠ENG=2x，根据三角形内角和得到x+2x+2x=180°，解得x=36°，于是得到∠F的度数的取值范围为0°＜x≤45°．

解答 解：（1）三角形的等腰线段如图所示，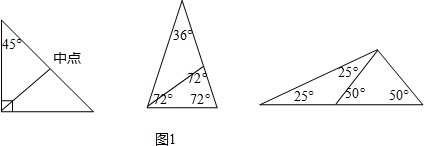

（2）设∠F=x，则∠G=2x，
如图2，线段EM是等腰线段，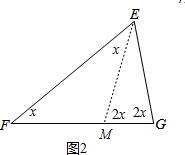
∵△EMG是等腰三角形，
∴EM=EG，ME=MF，
∴∠F=∠MEF=x，∠EMG=∠G=2x，
∴2x＜90°，
∴x＜45°；
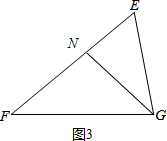
如图3，GN为等腰线段，
∴NF=NG，GN=GE，
∴∠F=∠NGF=x，∠E=∠ENG，
∴∠EGN=x，∠ENG=2x，
∴∠E=2x，
∴x+2x+2x=180°，
∴x=36°，
∴∠F的度数的取值范围为0°＜x≤45°．

点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图．也考查了等腰三角形的性质．