Question

18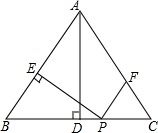．如图，在等腰△ABC中，AB=AC=5，BC=6，AD⊥BC于点D，动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动，过点P作PE⊥AB于点E，过点P作PF∥BA，交AC于点F，设点P运动的时间为t秒，若以PE所在直线为对称轴，线段BD经轴对称变换后的图形为B′D′，当线段B′D′与线段AC有公共点时，则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$．

Answer 1

分析 如图1中，当点B′与点A重合时．求出t的值．如图2中，当点D′在线段AC上时，求出t的值，由此即可求出t的取值范围．

解答 解：如图1中，当点B′与点A重合时．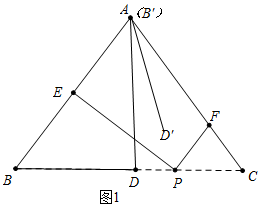

∵AB=AC=5，AD⊥BC，BC=6，
∴BD=DC=3，
在Rt△ABD中，cos∠B=$\frac{BD}{AB}$=$\frac{BE}{PB}$=$\frac{3}{5}$，
∵BE=AE=$\frac{5}{2}$，
∴$\frac{3}{5}$=$\frac{\frac{5}{2}}{PB}$，
∴PB=$\frac{25}{6}$，
∴此时t=$\frac{25}{6}$÷5=$\frac{5}{6}$，

如图2中，当点D′在线段AC上时．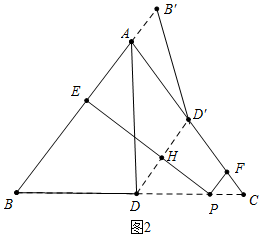

∵DD′⊥PE，AB⊥PE，
∴DD′∥AB，
∵BD=CD，
∴AD′=CD′，
∴DD′=$\frac{1}{2}$AB=$\frac{5}{2}$，
∴DH=$\frac{1}{2}$DD′=$\frac{5}{4}$，
∴∠HDP=∠B，
∴cos∠HDP=$\frac{DH}{DP}$=$\frac{3}{5}$，
∴DP=$\frac{25}{12}$，
∴BP=BD+DP=$\frac{61}{12}$，
∴此时t=$\frac{61}{12}$÷5=$\frac{61}{60}$，
∴当线段B′D′与线段AC有公共点时，则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$，
故答案为$\frac{5}{6}$≤t≤$\frac{61}{60}$．

点评 本题考查几何变换、等腰三角形的性质、锐角三角函数、勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，学会寻找特殊位置解决问题，属于中考填空题中的压轴题．