题目内容
2. 如图,点D,E分别为△ABC的边AB,AC上的中点,则△ADE的周长与△ABC的周长比为1:2.
如图,点D,E分别为△ABC的边AB,AC上的中点,则△ADE的周长与△ABC的周长比为1:2.
分析 D、E分别是AB、AC边的中点,则DE是△ABC的中位线;三角形的中位线平行于第三边,且等于第三边的一半,因而中位线分三角形得到的小三角形与原三角形一定相似,且相似是1:2,因而周长的比是1:2.
解答 解:∵点D,E分别为△ABC的边AB,AC上的中点,
∴AD=BD,AE=EC,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC
∵DE:BC=1:2
∴△ADE与△ABC的周长比为1:2,
故答案为:1:2.
点评 本题主要考查了三角形的中位线定理以及相似三角形的性质,掌握中位线定理及相似三角形的判定与性质是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
13.下列运算正确的是( )
| A. | x-3y=-2xy | B. | 5x2-2x2=3x2 | C. | x2+x3=x5 | D. | 2x2y-xy2=xy |
14.对一个三角形进行折叠,折痕是这个三角形角平分线的是( )
| A. |  | B. |  | C. |  | D. |  |
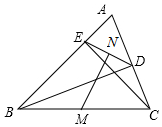 如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分别是BC,DE的中点.
如图,已知在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分别是BC,DE的中点.

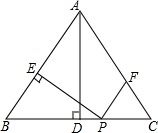 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.