题目内容
6. 如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.
如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.
分析 如图,设圆心为O′,作O′A⊥x轴于A,PD⊥x轴于D,O′F⊥PD于F.设优弧AP的圆心角为n.由弧长公式求出n,推出∠PO′A=120°,在Rt△PO′F中,求出PF,即可解决问题.
解答 解:如图,设圆心为O′,作O′A⊥x轴于A,PD⊥x轴于D,O′F⊥PD于F.设优弧AP的圆心角为n.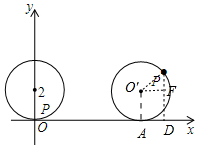
由题意$\frac{8}{3}$π=$\frac{n•π•2}{180}$,
解得n=240°,
∴∠PO′A=120°,
∵∠O′AD=∠FDA=∠O′FD=90°,
∴四边形O′ADE是矩形,
∴O′A=DF=2,∠FO′A=90°,
∴∠FO′P=30°,
在Rt△O′PF中,PF=$\frac{1}{2}$O′P=1,
∴PD=PF+DF=1+2=3,
∴点P到x轴的距离为3,
故答案为3.
点评 本题考查轨迹、弧长公式、坐标与图形的性质、矩形的判定和性质,直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
相关题目

 如图,点A在双曲线y=$\frac{k}{x}$(x>0)上,点B在直线y=-0.5x+5上,
如图,点A在双曲线y=$\frac{k}{x}$(x>0)上,点B在直线y=-0.5x+5上,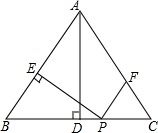 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒,若以PE所在直线为对称轴,线段BD经轴对称变换后的图形为B′D′,当线段B′D′与线段AC有公共点时,则t的取值范围是$\frac{5}{6}$≤t≤$\frac{61}{60}$.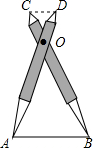 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短,如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A、B两个尖端分别在线段l的两个端点上,若CD=3.2cm,则AB的长为9.6cm.