题目内容
9.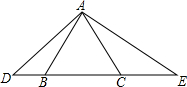 如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.
如图,等边三角形ABC中,D为CB延长线上一点,E为BC延长线上点,且满足∠DAE=120°.(1)求证:△ADB∽△EAC;
(2)若BD=1,AB=2,求DE的长.
分析 (1)由等边三角形的性质可知:∠ABC=∠ACB=60°,从而得到∠DBA=∠ECA=120°,然后再证明∠DAB=∠E,从而可证明△ADB∽△EAC;
(2)由相似三角形的性质可求得CE的长,然后根据ED=BD+CB+CE求解即可.
解答 解:(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°.
∴∠DBA=∠ECA=120°.
∵∠DAE=120°,
∴∠D+∠E=60°.
又∵∠D+∠DAB=60°,
∴∠DAB=∠E.
∴△ADB∽△EAC.
(2)∵△ADB∽△EAC,
∴$\frac{BD}{AB}=\frac{AC}{CE}$,即$\frac{1}{2}=\frac{2}{CE}$.
解得:CE=4.
∴DE=BD+BC+CE=1+2+4=7.
点评 本题主要考查的是相似三角形的性质和判定,掌握相似三角形的性质和判定定理是解题的关键.

练习册系列答案
相关题目
1.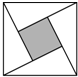 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形,如图,其直角三角形的两条直角边的长分别是2和4,则小正方形与大正方形的面积比是( )| A. | 1:2 | B. | 1:4 | C. | 1:5 | D. | 1:10 |
 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为50度.
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为50度.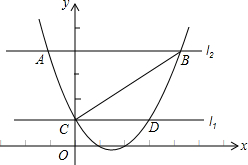 如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.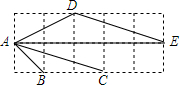 如图,在5×2的正方形网格中,小正方形的边长为1,△ABC与△ADE的顶点都在格点上.
如图,在5×2的正方形网格中,小正方形的边长为1,△ABC与△ADE的顶点都在格点上.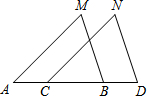 如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.
如图,已知A、B、C、D在同一直线上,AM=CN,MA∥NC,∠M=∠N,证明:AC=BD.