题目内容
3．
如图，平面直角坐标系中，已知点A（-3，2），点B（3，6），则△AOB的面积为12．
分析 根据A、B的坐标在平面直角坐标系中确定出三角形AOB，可以表示出S△AOB=$\frac{（2+6）×6}{2}-\frac{2×3}{2}-\frac{3×6}{2}=12$，就可以求出S△AOB的值．
解答 解：根据题意画图象得，
S△AOB=$\frac{（2+6）×6}{2}-\frac{2×3}{2}-\frac{3×6}{2}=12$，
故答案为：12
点评 本题主要考查了坐标与图形关系，关键是根据点的坐标的求法和三角形面积的求法分析．
练习册系列答案
相关题目
如图，AB是半圆的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD，求证：直线PD是⊙O的切线．
如图，已知两个正方形，请画出一个新的正方形使其面积等于已知两个正方形的面积之和．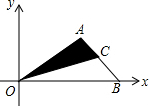
已知如图所示，A（3，2）、B（5，0）、C（4，1），则△AOC的面积为$\frac{5}{2}$．
如图，已知∠BAC，用直尺和圆规作图：