题目内容
10. 如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.
如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.
分析 要证是直线PD是为⊙O的切线,需证∠PDO=90°.因为AB为直径,所以∠ADO+∠ODB=90°,由∠PDA=∠PBD=∠ODB可得∠ODA+∠PDA=90°,即∠PDO=90°.
解答 证明:∵OB=OD,
∴∠ODB=∠PBD,
∵AB为直径,
∵∠ADB=90°,
∴∠ADO+∠ODB=90°.
∵∠PDA=∠PBD=∠ODB,
∴∠ODA+∠PDA=90°.即∠PDO=90°.
∴OD⊥PD,
∴PD是⊙O的切线.
点评 本题考查了圆周角定理、等边三角形的判定与性质、切线的判定;证明OD⊥PD是解决问题的关键.

练习册系列答案
相关题目
5. 如图所示的立体图形,它的主视图是( )
如图所示的立体图形,它的主视图是( )
 如图所示的立体图形,它的主视图是( )
如图所示的立体图形,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
15.某药品经过两次降价,每瓶零售价由180元降为100元.已知两次降价的百分率相同,设每次降价的进分率为x,根据题意列方程正确的是( )
| A. | 180(1+x)2=100 | B. | 180(1-x2)=100 | C. | 180(1-2x)=100 | D. | 180(1-x)2=100 |
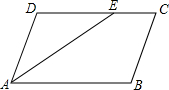 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F. 如图,已知抛物线y=x2-2x+2与y轴交于点A.
如图,已知抛物线y=x2-2x+2与y轴交于点A.
 如图,平面直角坐标系中,已知点A(-3,2),点B(3,6),则△AOB的面积为12.
如图,平面直角坐标系中,已知点A(-3,2),点B(3,6),则△AOB的面积为12.