题目内容
18．
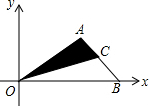已知如图所示，A（3，2）、B（5，0）、C（4，1），则△AOC的面积为$\frac{5}{2}$．
分析 根据点的坐标得到AE=2，CD=1，OB=5，再由图形可知△AOC的面积=△ABC的面积-△BOC的面积，即可解答．
解答 解：如图，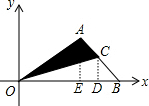
过点C作CD⊥OB于点D，过点A作AE⊥OB于点E，
∵A（3，2）、B（5，0）、C（4，1），
∴AE=2，CD=1，OB=5，
∴S△AOC=S△ABC-S△BOC=$\frac{1}{2}OB•AE=\frac{1}{2}OB•CD$=$\frac{1}{2}×5×2-\frac{1}{2}×5×1=5-\frac{5}{2}=\frac{5}{2}$．
故答案为：$\frac{5}{2}$．
点评 本题考查了坐标与图形性质，解决本题的关键是明确△AOC的面积=△ABC的面积-△BOC的面积．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
5．
如图所示的立体图形，它的主视图是（ ）
如图所示的立体图形，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
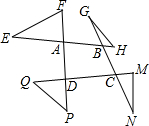如图，以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ，求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数．
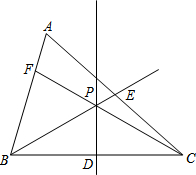如图所示，直线PD为△ABC一边BC的垂直平分线，点D为垂足，连接CP并延长CP交边AB于点F，射线BP交边AC于点E．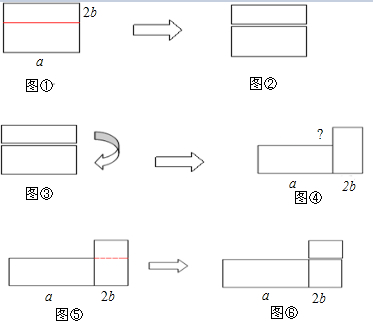
如图，平面直角坐标系中，已知点A（-3，2），点B（3，6），则△AOB的面积为12．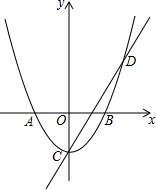
如图，在平面直角坐标系中，抛物线与x轴交于点A（-1，0）和点B（1，0），直线y=2x-1与y轴交于点C，与抛物线交于点C、D．
从而可得该不等式组的解集为1≤x＜4．