题目内容
14.下列运算中,正确的是( )| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
分析 分别利用二次根式的性质化简各数进而求出即可.
解答 解:A、$\sqrt{3+4}$=$\sqrt{7}$,故此选项错误;
B、$\sqrt{4-3}$=1,故此选项错误;
C、$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,故此选项错误;
D、$\sqrt{(4+3)^{2}}$=4+3,正确.
故选:D.
点评 此题主要考查了二次根式的化简,正确利用二次根式的性质得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
 如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )
如图,已知△ABC∽△ADE,∠AED=40°,∠B=80°,则∠A的度数为( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
3.已知一元二次方程x2-2x+3=0的两根为a,b,则$\frac{1}{a}+\frac{1}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 以上答案都不对 |
 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.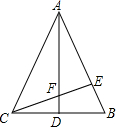 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.
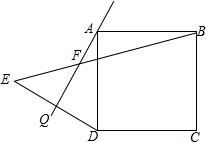 在小学,我们已经初步了解到,正方形的每个角都是90°,每个边都是相等.如图,在正方形ABCD外侧作直线AQ,点D关于直线AQ的对称点为E,连接DE、BE,BE交AD于点F,若∠QAD=15°.
在小学,我们已经初步了解到,正方形的每个角都是90°,每个边都是相等.如图,在正方形ABCD外侧作直线AQ,点D关于直线AQ的对称点为E,连接DE、BE,BE交AD于点F,若∠QAD=15°.