题目内容
3.已知一元二次方程x2-2x+3=0的两根为a,b,则$\frac{1}{a}+\frac{1}{b}$的值为( )| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 以上答案都不对 |
分析 根据根与系数的关系得到a+b=2,ab=3,再把原式变形得到$\frac{a+b}{ab}$,然后利用整体代入的方法进行计算.
解答 解:∵一元二次方程x2-2x+3=0的两根为a,b,
∴a+b=2,ab=3,
∴原式=$\frac{a+b}{ab}$=$\frac{2}{3}$.
故选A.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.某公司的仓库中原先有1.5万件货物,后又运出0.7万件,过了一段时间后计划往仓库中补充1.2万件,但因为某些原因,少往仓库中补充0.3万件,则现在仓库中的货物有( )
| A. | 1.8万件 | B. | 1.7万件 | C. | 1.5万件 | D. | 1.1万件 |
14.下列运算中,正确的是( )
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
12.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )
| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O 内 | D. | 不能确定 |
13.如表
从左到右每小格中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2014个格子与第2015个格子中的数之和为2.
| 3 | a | b | c | -1 | 2 | … |
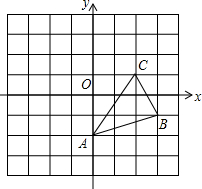 将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.