题目内容
6.如图,数轴上点A、C对应的数分别为a,c,且a,c满足|a+b|+(c-1)2014=0,点B对应的数为-3,(1)求数a,c;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,设运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值;
(3)在(2)的条件下,点B运动到点C后立即以原速返回,到达自己的出发点后停止运动,点A运动至点C后也以原速返回,到达自己的出发点后又折返向点C运动,当点B停止运动时,点A随之停止运动,求在此运动过程中,A,B两点同时到达的点在数轴上所表示的数.

分析 (1)根据非负数的和为0的定理建立方程求出其解;
(2)根据A,B两点到原点O的距离相等分两种情况:当A、B在原点的左侧A、B相遇时和A、B在原点的异侧时,建立方程求出其解即可;
(3)第一次同时到达的点是A追上B的地方,第二次同时到达的点是A返回的过程中与A相遇的地方,第三次相遇是B在返回的过程中与A相遇的地方,第五次相遇是A追上B的地方,第六次相遇的A返回与B相遇的地方.
解答 解:(1)由题意,得
a+4=0,c-1=0,
解得:a=-4,c=1
答:a对应的数为-4,b对应的数为1;
(2)∵点B对应的数为-3,A对应的数是-4,
∴AB=1.AO=4,BO=3.
当A、B在原点的左侧A、B相遇时,
2t-t=1,
t=1,
当A、B在原点的异侧时,
2t-4=3-t,
解得:t=$\frac{7}{3}$.
∴A,B两点到原点O的距离相等时,t的值为1或$\frac{7}{3}$.
(3)由(2)得,
当t=1时,A,B两点同时到达的点是-2;
2.5秒时A点对应的数是1,B点对应的数是-0.5,
∴AB=1.5,
设过t秒A、B相遇,由题意得
2t+t=1.5,
解得:t=0.5,
此时A,B两点同时到达的点是0.
再过两秒时A到达A点,B返回在0,
∴AB=4,设A、B再过t秒相遇,由题意,得
2t+t=4,
t=$\frac{4}{3}$,
此时A,B两点同时到达的点是-$\frac{4}{3}$.在此3秒时,A为0,B为-3.
∴A,B两点同时到达的点在数轴上表示的数为:-2,0,-$\frac{4}{3}$.
点评 本题考查了一元一次方程的运用,数轴的运用,绝对值的运用,偶次幂的运用,解答时根据行程问题的追击问题和相遇问题的数量关系建立方程是关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
17.已知关于x的一元二次方程x2-x-1=0的两根分别为x1、x2,则|x1-x2|的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
14.下列运算中,正确的是( )
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
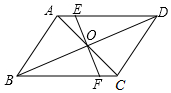 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.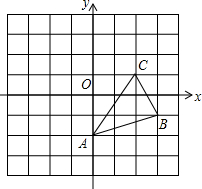 将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.
将图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化.