题目内容
5. 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:△ABC≌△DCB.
分析 首先根据角平分线的性质可得∠ACB=∠DBC,然后再加上公共边BC=BC可利用ASA定理判定△ABC≌△DCB.
解答 证明:∵∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线,
∴∠ACB=∠DBC,
在△ABC和△DCB中,
$\left\{\begin{array}{l}{∠ACB=∠DBC}\\{BC=BC}\\{∠ABC=∠DCB}\end{array}\right.$,
∴△ABC≌△DCB(ASA).
点评 此题主要考查了三角形全等的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某公司的仓库中原先有1.5万件货物,后又运出0.7万件,过了一段时间后计划往仓库中补充1.2万件,但因为某些原因,少往仓库中补充0.3万件,则现在仓库中的货物有( )
| A. | 1.8万件 | B. | 1.7万件 | C. | 1.5万件 | D. | 1.1万件 |
17.已知关于x的一元二次方程x2-x-1=0的两根分别为x1、x2,则|x1-x2|的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
14.下列运算中,正确的是( )
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
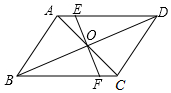 如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
如图,已知AB∥CD,AD∥BC,过AC和BD的交点O的直线EF分别交AD、BC于E、F,则图中全等三角形一共有( )对.
