题目内容
9.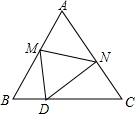 如图,在等边三角形纸片△ABC中,将纸片折叠,点A落在BC边上的点D处,MN为折痕,当DN⊥NC时,CN=1,则A、D两点之间的距离为$\sqrt{6}$.
如图,在等边三角形纸片△ABC中,将纸片折叠,点A落在BC边上的点D处,MN为折痕,当DN⊥NC时,CN=1,则A、D两点之间的距离为$\sqrt{6}$.
分析 首先根据轴对称的性质,可得AN=DN,然后在Rt△NDC中,利用60°角求得DN=$\sqrt{3}$,CN=$\sqrt{3}$;最后在Rt△ADN中,根据勾股定理,求出AD的长度,即可判断出A、D两点之间的距离为多少.
解答 解:∵DN⊥NC,
∴DN=CN•tan60°=$\sqrt{3}$,
∴AN=$\sqrt{3}$,
∴AD=$\sqrt{{(\sqrt{3})}^{2}{+(\sqrt{3})}^{2}}$=$\sqrt{6}$,
即A、D两点之间的距离为$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知∠A,∠B互补,∠A比∠B大60°,设∠A,∠B的度数分别为x°,y°,下列方程组中符合题意的是( )
| A. | $\left\{\begin{array}{l}{x+y=180}\\{x=y-60}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{x=y+60}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=90}\\{x=y-60}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=90}\\{x=y+60}\end{array}\right.$ |
4.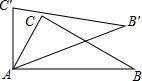 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
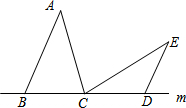 如图:在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE,点B,C,D在直线m上.以点C为旋转中心,将△CDE按逆时针方向旋转,使得CE与CA重合,得到△CD1E1(A).
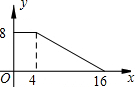
如图:在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE,点B,C,D在直线m上.以点C为旋转中心,将△CDE按逆时针方向旋转,使得CE与CA重合,得到△CD1E1(A).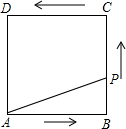 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )
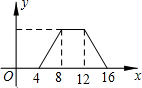
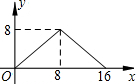
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )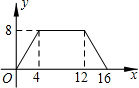
 如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.
如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.