题目内容
5.已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、DE交AB于点M.(1)如图1,当E、A、F在一直线上时,求证:点M为ED中点;
(2)如图2,当AF∥ED,求证:AM2=AB•BM.

分析 (1)连接AC,根据正方形的性质得到∠DAM=∠BEM=∠BCD=90°,根据全等三角形的判定和性质即可得到结论;
(2)根据正方形的性质得到∠DAM=∠EBM=90°,AD=AB,根据相似三角形的性质得到$\frac{AM}{BM}$=$\frac{AD}{BE}$,根据已知条件得到四边形AMDF是平行四边形,根据平行四边形的性质得到AM=DF,等量代换得到AM=BE,于是得到结论.
解答 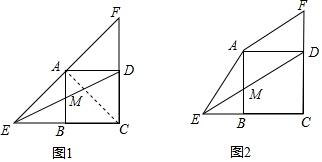 (1)连接AC,∵四边形ABCD是正方形,
(1)连接AC,∵四边形ABCD是正方形,
∴∠DAM=∠BEM=∠BCD=90°,∠BCA=∠DCA=45°,AB=BC=CD=DA,
∵BE=DF,∴CE=CF,
∴∠AEB=∠F=45°,
∴BE=BA=AD,
在△ADM和△BEM中,$\left\{\begin{array}{l}{∠DAM=∠EBM}\\{∠AMD=∠BME}\\{AD=BE}\end{array}\right.$,
∴△ADM和△BEM,
∴DM=EM,即点M为ED中点;
(2)解:∵四边形ABCD是正方形,
∴∠DAM=∠EBM=90°,AD=AB,
∴△ADM∽△BEM,
∴$\frac{AM}{BM}$=$\frac{AD}{BE}$,
∵AM∥DF,AF∥DE,
∴四边形AMDF是平行四边形,
∴AM=DF,
∵BE=DF,
∴AM=BE,
∴$\frac{AM}{BM}=\frac{AB}{AM}$,
∴AM2=AB•BM.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行四边形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
16.下列运算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | (a+b)2=a2+b2 | C. | (a2+5)0=1 | D. | (-a2)3=a6 |
13. 如图,一块飞镖游戏板由大小相等的小正方形网格构成.向游戏板随机投中一枚飞镖,击中黑色区域的概率是( )
如图,一块飞镖游戏板由大小相等的小正方形网格构成.向游戏板随机投中一枚飞镖,击中黑色区域的概率是( )
 如图,一块飞镖游戏板由大小相等的小正方形网格构成.向游戏板随机投中一枚飞镖,击中黑色区域的概率是( )
如图,一块飞镖游戏板由大小相等的小正方形网格构成.向游戏板随机投中一枚飞镖,击中黑色区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
17.下列说法不正确的是( )
| A. | 调查一架“歼20”隐形战机各零部件的质量,应采用抽样调查 | |
| B. | 一组数据2,2,3,3,3,4的众数是3 | |
| C. | 如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是7 | |
| D. | 一组数据1,2,3,4,5的方差是2,那么数据11,12,13,14,15的方差也是2 |
14.把二次根式$\sqrt{\frac{27}{2}}$化简成最简二次根式,结果为( )
| A. | 3$\sqrt{\frac{3}{2}}$ | B. | 9$\sqrt{\frac{1}{6}}$ | C. | $\frac{\sqrt{54}}{2}$ | D. | $\frac{3\sqrt{6}}{2}$ |
15.-9的相反数是( )
| A. | 9 | B. | -9 | C. | -$\frac{1}{9}$ | D. | $\frac{1}{9}$ |
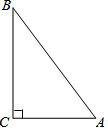 已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.
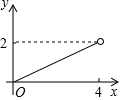
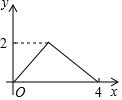
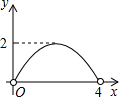
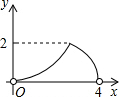
已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.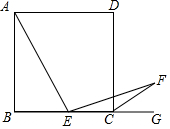 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交正方形的外角∠DCG的平分线于点F,设BE=x,△ECF的面积为y,下列图象中,能大致表示y与x的函数关系的是( )
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交正方形的外角∠DCG的平分线于点F,设BE=x,△ECF的面积为y,下列图象中,能大致表示y与x的函数关系的是( )