题目内容
20.若一个两位正整数m的个位数为8,则称m为“好数”.(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定:H(m)=$\frac{q}{p}$,例如68=182-162,称数对(18,16)为“友好数对”,则H(68)=$\frac{16}{18}$=$\frac{8}{9}$,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
分析 (1)设m=10t+8,1≤t≤9,且t为整数,由于m2-64=20(5t2+8t),于是得到结论;
(2)根据已知条件得到10t+8=(p+q)(p-q),于是得到H(28)=$\frac{6}{8}=\frac{3}{4}$,H(48)=$\frac{11}{13}$或H(48)=$\frac{4}{8}$=$\frac{1}{2}$或H(48)=$\frac{1}{7}$,即可得到结论.
解答 (1)证明:设m=10t+8,1≤t≤9,且t为整数,
∴m2-64=(10t+8)2-64=100t2+160t+64-64=20(5t2+8t),
∵1≤t≤9,且t为整数,
∴5t2+8t是正整数,
∴m2-64一定为20的倍数;
(2)解:∵m=p2-q2,且p,q为正整数,
∴10t+8=(p+q)(p-q),
当t=1时,18=1×18=2×9=3×6,没有满足条件的p,q;
当t=2时,28=1×28-3×14=4×7,
其中满足条件的p,q的数对有(8,6),即28=82-62,
∴H(28)=$\frac{6}{8}=\frac{3}{4}$,
当t=3时,38=1×38=2×19,没有满足条件的p,q;
当t=4时,48=1×48=2×24=3×16=4×12=6×8,
满足条件的p,q的数对为$\left\{\begin{array}{l}{p-q=2}\\{p+q=24}\end{array}\right.$或$\left\{\begin{array}{l}{p-q=4}\\{p+q=12}\end{array}\right.$或$\left\{\begin{array}{l}{p-q=6}\\{p+q=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{p=13}\\{q=11}\end{array}\right.$或$\left\{\begin{array}{l}{p=8}\\{q=4}\end{array}\right.$或$\left\{\begin{array}{l}{p=7}\\{q=1}\end{array}\right.$,
即48=132-92=82-42=72-12,
∴H(48)=$\frac{11}{13}$或H(48)=$\frac{4}{8}$=$\frac{1}{2}$或H(48)=$\frac{1}{7}$,
∵$\frac{11}{13}>\frac{3}{4}>\frac{1}{2}>\frac{1}{7}$,
∴H(m)的最大值为$\frac{11}{13}$.
点评 本题考查了因式分解的应用,正确的理解”好数”和“友好数对”是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | x2•x3=x6 | B. | (x3)2=x5 | C. | (-2x2y)3=-8 x6y3 | D. | -x+2x=-3x |
| A. | a>4 | B. | a<4 | C. | a≤4 | D. | a<4,且a≠0 |
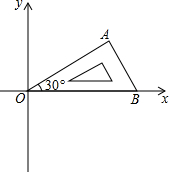 将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=4,将三角板绕原点O逆时针旋转,每秒旋转60°,则第2017秒时,点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB按如图所示的方式放置在平面直角坐标系中,OB在x轴上,若OA=4,将三角板绕原点O逆时针旋转,每秒旋转60°,则第2017秒时,点A的对应点A′的坐标为( )| A. | (0,4) | B. | (2$\sqrt{3}$,-2) | C. | (-2$\sqrt{3}$,2) | D. | (0,-4) |
| A. | x+x2=x3 | B. | 3x-2x=1 | C. | (x2)3=x6 | D. | x6÷x3=x2 |
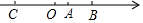 如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24.
如图,已知A,B,C是数轴上三点,O为原点,点A点B在原点的右侧,点C在原点的左侧,点A表示的数为m,若关于x 的多项式-x3+12x2-3mx2-2x+4不含x2,且AB=6,AC=24. 如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$.
如图所示,等边三角形ABC的边长为4$\sqrt{3}$,过点A作AD⊥AB,AD=2,以AD为边在AD左侧作菱形ADEF,∠DAF=60°.连接BE,点G为线段BE的中点,连接DG,CG,则线段DG=$\sqrt{7}$,CG=$\sqrt{21}$.