题目内容
18. 已知∠A0B=30°,M为0B上一点,且0M=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
已知∠A0B=30°,M为0B上一点,且0M=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?(1)r=2cm.(2)r=4cm.(3)r=2.5cm.
分析 作MC⊥OA于C,则∠OCM=90°,由含30°角的直角三角形的性质得出MC=$\frac{1}{2}$OM=2.5cm,即圆心到直线OA的距离d=2.5cm;若d<r,则直线与圆相交;若d=r,则直线与圆相切;若d>r,则直线与圆相离;即可得出结果.
解答 解:作MC⊥OA于C,如图所示:
则∠OCM=90°,
∵∠AOB=30°,
∴MC=$\frac{1}{2}$OM=2.5cm,
即圆心到直线OA的距离d=2.5cm,
(1)当r=2cm时,d>r,
∴⊙M与直线OA相离;
(2)当r=4cm时,d<r,
∴⊙M与直线OA相交;
(3)当r=2.5cm时,d=r,
∴⊙M与直线OA相切.
点评 本题考查了直线与圆的位置关系、含30°角的直角三角形的性质;能够熟练根据数量关系判断直线和圆的位置关系是解题的关键.

练习册系列答案
相关题目
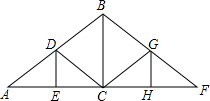 如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,当DE=1.85m,∠A=30°时,求斜梁AB的长.
如图,是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,当DE=1.85m,∠A=30°时,求斜梁AB的长. 如图,已知一艘轮船有西向东航行,航行到A处测得小岛P的方向是北偏东75°,又航行10海里后.在B处测得小岛P的方向是北偏东60°,若小岛周围4.8海里内有暗礁.问:该轮船一直向东航行是否有触礁的危险!
如图,已知一艘轮船有西向东航行,航行到A处测得小岛P的方向是北偏东75°,又航行10海里后.在B处测得小岛P的方向是北偏东60°,若小岛周围4.8海里内有暗礁.问:该轮船一直向东航行是否有触礁的危险!