题目内容
18.若$\sqrt{x-2}$+$\sqrt{2-x}$+y2+4y=-2x,求2x-y的值.分析 根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,解得:x=2,然后再把x=2代入$\sqrt{x-2}$+$\sqrt{2-x}$+y2+4y=-2x可得y的值,进而可得答案.
解答 解:由题意得:$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,
解得:x=2,
∵$\sqrt{x-2}$+$\sqrt{2-x}$+y2+4y=-2x,
∴$\sqrt{x-2}$+$\sqrt{2-x}$+y2+4y+2x=0,
∴y2+4y+4=0,
(y+2)2=0,
y=-2,
∴2x-y=4-(-2)=6.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式有意义,被开方数为非负数.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3. 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
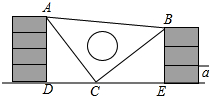 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.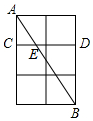 如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.
如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.