题目内容
9.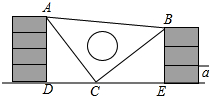 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知DE=42cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等)
分析 (1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可.
(2)利用(1)中全等三角形的性质进行解答.
解答 (1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS);
(2)解:由题意得:∵一块墙砖的厚度为a,
∴AD=4a,BE=3a,
由(1)得:△ADC≌△CEB,
∴DC=BE=3a,AD=CE=4a,
∴DC+CE=BE+AD=7a=42,
∴a=6,
答:砌墙砖块的厚度a为6cm.
点评 此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.一元二次方程x2-9=0的根是( )
| A. | x=3 | B. | x=-3 | C. | x1=3,x2=-3 | D. | x1=9,x2=-9 |
20.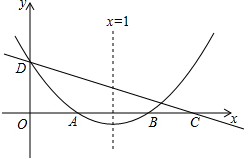 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
①abc>0; ②3a+b>0; ③-1<k<0; ④4a+2b+c<0; ⑤a+b<k.
 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( )①abc>0; ②3a+b>0; ③-1<k<0; ④4a+2b+c<0; ⑤a+b<k.
| A. | ①②③ | B. | ②③⑤ | C. | ②④⑤ | D. | ②③④⑤ |
19.已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
(1)根据上表填空:
①这个抛物线的对称轴是x=1,抛物线一定会经过点(-2,10 );
②抛物线在对称轴右侧部分是上升(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
| x | … | -1 | 0 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 2 | 5 | 10 | … |
①这个抛物线的对称轴是x=1,抛物线一定会经过点(-2,10 );
②抛物线在对称轴右侧部分是上升(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.