题目内容
6.已知1+$\sqrt{{b}^{2}-4}$=4a-4a2,求ab的值.分析 将已知等式进行变形得到(2a-1)2+$\sqrt{{b}^{2}-4}$=0,由非负数的性质可以求得a、b的值;然后代入ab求值即可.
解答 解:∵1+$\sqrt{{b}^{2}-4}$=4a-4a2,
∴(2a-1)2+$\sqrt{{b}^{2}-4}$=0,
∴2a-1=0,b2-4=0,
则a=$\frac{1}{2}$,b=±2,
则ab=($\frac{1}{2}$)2=$\frac{1}{4}$或ab=($\frac{1}{2}$)-2=4.
点评 本题考查了配方法的应用,非负数的性质.利用条件得出(2a-1)2+$\sqrt{{b}^{2}-4}$=0是解题的关键.

练习册系列答案
相关题目
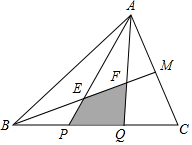 如图,S△ABC=1,AM=MC,BP=PQ=QC,求阴影部分的面积.
如图,S△ABC=1,AM=MC,BP=PQ=QC,求阴影部分的面积.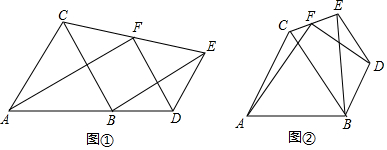 如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.
如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.