题目内容
12.如图1,已知直线y=-3x+6与x轴、y轴交于A、B两点,点C在x轴负半轴上,S△BOC=3S△BOA(1)求直线BC的函数表达式;
(2)如图2,一条直线y=mx经过原点,与直线AB,BC分别交于点E、F,若S△BOE=S△BOF,求m的值;
(3)如图3,将(2)中直线EF向上平行移动后经过点B,与x轴交于点G,设H为线段BG上一点(含端点),连接AH,一动点M从点A出发,沿线段AH运动到H,再沿线段HB运动到B后停止,若点M在AH上的速度为每秒1个单位,在HB上的速度为每秒$\sqrt{2}$个单位,当点H的坐标是多少时,点M在整个运动过程中用时最少?

分析 (1)根据轴上S△BOC=S△AOB可以求出点C坐标,用待定系数法即可求出直线BC的解析式.
(2)利用方程组求出点E、F坐标,根据题意OE=OF,说明E、F两点的横坐标互为相反数,由此可以求出m.
(3)作BP⊥y轴,AK⊥BP垂足为K,因为点M从A→H→B的时间t=$\frac{AH}{1}$+$\frac{BH}{\sqrt{2}}$=AH+HK=AK,AK是点A到直线BP的垂线段,根据垂线段最短,点H就是所找的点,这样点H的坐标就不难求出来了.
解答 解:(1)∵直线y=-3x+6与x轴、y轴交于A、B两点,
∴A(2,0),B(0,6),
∵S△BOC=3S△AOB,
∴$\frac{1}{2}$×CO×6=3×$\frac{1}{2}$×2×6,
∴CO=6,
∴点C坐标(-6,0),
设直线BC为y=kx+b,B、C两点坐标分别代入得$\left\{\begin{array}{l}{b=6}\\{-6k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=6}\end{array}\right.$,
∴直线BC解析式为y=x+6.
(2)由$\left\{\begin{array}{l}{y=mx}\\{y=x+6}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{6}{m-1}}\\{y=\frac{6m}{m-1}}\end{array}\right.$,故F点坐标为($\frac{6}{m-1}$,$\frac{6m}{m-1}$),
由$\left\{\begin{array}{l}{y=mx}\\{y=-3x+6}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{6}{m+3}}\\{y=\frac{6m}{m+3}}\end{array}\right.$,故E点坐标为($\frac{6}{m+3}$,$\frac{6m}{m+3}$),
∵S△BOE=S△BOF,
∴OF=OE,
∴$\frac{6}{m-1}+\frac{6}{m+3}=0$,
解得m=-1,经过检验x=-1是分式方程的解,
故m=-1.
(3)如图作BP⊥y轴,AK⊥BP垂足为K,交BG于H,此时点M从A→H→B用时最少.
理由:∵直线EF为y=-x,
∴∠AOF=∠COF=45°,
∵BG∥EF,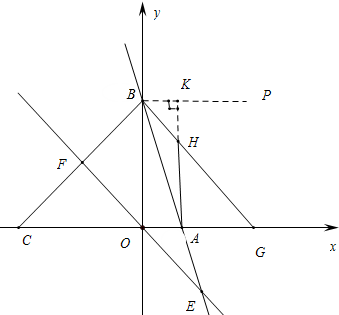
∴∠GBO=∠BOF=45°,
∵∠PBO=45°,
∴∠KBH=∠BHK=45°,
∴KH=$\frac{BH}{\sqrt{2}}$,
∴点M从A→H→B的时间t=$\frac{AH}{1}$+$\frac{BH}{\sqrt{2}}$=BH+HK=AK,
∵AK⊥BP,
∴垂线段AK最短,故点M从A→H→B用时最少,
∵∠AOB=∠OBK=∠AKB=90°,
∴四边形AOBK是矩形,
∴AK=BO=6,OA=BK=2,
∴BK=HK=2,AH=4,
∴H(2,4).
点评 本题考查一次函数图象与性质、待定系数法、用方程组求交点坐标、垂线段最短、矩形以及等腰直角三角形的性质等知识,灵活运用垂线段最短是解决最后一个问题的关键.

 芳芳有一个无盖的收纳箱,该收纳箱展开后的图形(实线部分)如图所示,将该图形补充四个边长为10cm的小正方形后,得到一个矩形,已知矩形的面积为2000cm2,根据图中信息,可得x的值为( )
芳芳有一个无盖的收纳箱,该收纳箱展开后的图形(实线部分)如图所示,将该图形补充四个边长为10cm的小正方形后,得到一个矩形,已知矩形的面积为2000cm2,根据图中信息,可得x的值为( )| A. | 10 | B. | 20 | C. | 25 | D. | 30 |
| A. | (-2)2<-22 | B. | -$\frac{4}{5}$>-$\frac{7}{6}$ | C. | -0.3<-$\frac{1}{3}$ | D. | -$\frac{10}{9}$>-$\frac{9}{10}$ |
| A. | x+a=y+a | B. | $\frac{x}{a}=\frac{y}{a}$ | C. | x-a=y-a | D. | ax=ay |
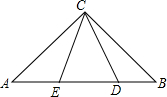 如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )
如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )