题目内容
2.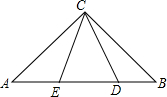 如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )
如图,在Rt△ABC中,AC=BC,点D,E在斜边AC上,且满足AE=4,BD=3,∠DCE=45°,则DE的长度为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
分析 如图,将△ACE绕点C逆时针旋转90°到△CBF的位置;证明∠A=∠ABC=∠CBF=45°,得到DF2=AE2+BD2,进一步证明△ECD≌△FCD,得到DE=DF,得出DE2=AE2+BD2解决问题.
解答 解:如图,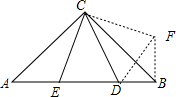
将△AEC绕点C逆时针旋转90°到△CBF的位置;
则CD=CF,AE=BF;∠BCF=∠ACE,∠CBF=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBF=45°,
∴∠DBF=90°DEF2=BD2+BF2=AE2+BD2;
∵∠DCE=45°,∠ACB=90°,
∴∠ACE+∠BCD=90°-45°=45°,而∠ACE=∠BCF,
∴∠DCF=∠DCE=45°;
在△DCE与△FCD中,
$\left\{\begin{array}{l}{CE=CD}\\{∠ECD=∠FCD}\\{CD=CD}\end{array}\right.$,
∴△ECD≌△FCD(SAS),
∴DE=DF,
∴DE2=AE2+BD2=42+32=25,
∴DE=5.
故选:C.
点评 此题主要考查了旋转变换的性质、全等三角形的判定及其性质、勾股定理;解题的关键是作旋转变换,把问题转换,进一步利用三角形全等的判定与性质以及勾股定理解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.x的m次方的5倍与x2的7倍的积是( )
| A. | 12x2m | B. | 35x2m | C. | 35xm+2 | D. | 12xm+2 |
 如图,在平面直角坐标系中,抛物线交y轴于点A(0,3),交x轴于点B(2,0),点C(6,0),(点B在点C的左侧),过点B作线段AB的垂线交抛物线于点D.
如图,在平面直角坐标系中,抛物线交y轴于点A(0,3),交x轴于点B(2,0),点C(6,0),(点B在点C的左侧),过点B作线段AB的垂线交抛物线于点D. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以AB为直径作半圆O交BC于点D,过点D的切线交AC于点E,BE交⊙O于点F,AF的延长线与DE相交于点P.若OA=l,则EB=$\sqrt{7}$,PE=$\frac{12-2\sqrt{3}}{11}$.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以AB为直径作半圆O交BC于点D,过点D的切线交AC于点E,BE交⊙O于点F,AF的延长线与DE相交于点P.若OA=l,则EB=$\sqrt{7}$,PE=$\frac{12-2\sqrt{3}}{11}$.
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.