题目内容
4．
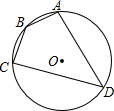如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D=45°，则劣弧AC的长为π．
分析 连接OA、OC，然后根据圆周角定理求得∠AOC的度数，最后根据弧长公式求解．
解答 
解：连接OA、OC，
∵∠D=45°，
∴∠AOC=2∠D=90°，
则劣弧AC的长为：$\frac{90π×2}{180}$=π．
故答案为π．
点评 本题考查了弧长的计算以及圆周角定理，解答本题的关键是掌握弧长公式l=$\frac{nπr}{180}$．
练习册系列答案
相关题目
14．在有理数1、-2、-$\frac{1}{2}$、0中，最小的数是（ ）
| A． | 1 | B． | -2 | C． | -$\frac{1}{2}$ | D． | 0 |
15．
有理数a、b在数轴上的对应点的位置如图所示，则下列正确的是（ ）
有理数a、b在数轴上的对应点的位置如图所示，则下列正确的是（ ）| A． | a+b=0 | B． | a+b＞0 | C． | |a|＞|b| | D． | a-b＞0 |
如图是由五个相同的小立方块搭成的几何体，则它的主视图是（ ）
16．点B与点A（-2，3）关于原点对称，点B的坐标为（ ）
| A． | （2，-3） | B． | （-2，3） | C． | （2，3） | D． | （-2，-3） |
13．⊙O是等边△ABC的外接圆，⊙O的半径为4，则等边△ABC的边长为（ ）
| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{5}$ | C． | 4$\sqrt{3}$ | D． | 4$\sqrt{5}$ |