Question

1．如图，平行四边形ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x²-7x+12=0的两个根，且OA＞OB
（1）求cos∠ABC的值．
（2）若E为x轴上的点，且S_△AOE=$\frac{16}{3}$，求出点E的坐标，并判断△AOE与△DAO是否相似？请说明理由．

Answer 1

分析 （1）用因式分解法解出一元二次方程，求出OA、OB的长，即可求得cos∠ABC的值；
（2）设点E的坐标为（m，0），根据三角形的面积公式求出m的值，得到点E的坐标；再求出$\frac{OA}{DA}$和$\frac{OE}{OA}$的值，根据两组对应边成比例并且夹角相等的两个三角形相似证明结论．

解答 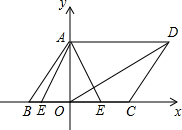解：（1）x²-7x+12=0，
（x-3）（x-4）=0，
解得x₁=3，x₂=4，
∴OA=4，OB=3，
∴Rt△AOB中，AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴cos∠ABC=$\frac{OB}{AB}$=$\frac{3}{5}$；

（2）设点E的坐标为（m，0），则
$\frac{1}{2}$×|m|×4=$\frac{16}{3}$，
解得m=±$\frac{8}{3}$，
∴点E的坐标为：（$\frac{8}{3}$，0）或（-$\frac{8}{3}$，0）；

△AOE∽△DAO．
理由：∵$\frac{OE}{OA}$=$\frac{2}{3}$，=$\frac{OA}{AD}$=$\frac{2}{3}$，
∴$\frac{OE}{OA}$=$\frac{OA}{AD}$，
又∵∠AOE=∠DAO=90°，
∴△AOE∽△DAO．

点评 本题属于四边形综合题，主要考查的是一元二次方程的解法、解直角三角形以及相似三角形的判定的综合应用，掌握因式分解法解一元二次方程和相似三角形的判定定理是解题的关键．