题目内容
6．
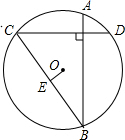如图所示，已知⊙O弦AB⊥CD，OE⊥BC于点E，求证：AD=2OE．
分析 根据三角形的中位线，可得OE与CF的关系，根据平行线的判定与性质，可得$\widehat{AD}$与$\widehat{CF}$，根据等弧所对的弦相等，可得AD与CF的关系，根据等量代换，可得答案．
解答 证明：作直径BF，连接AF，CF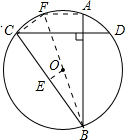
，
∵OE⊥BC
∴BE=CE
∵BO=FO
∴OE=$\frac{1}{2}$CF．
∵BF 是直径
∴∠BAF=90°
∵AB⊥CD
∴AF‖CD
∴$\widehat{AD}$=$\widehat{CF}$
∴AD=FC
∵OE=$\frac{1}{2}$CF
∴OE=$\frac{1}{2}$AD
∴AD=2OE．
点评 本题考查了圆周角定理，利用了三角形中位线定理，平行线所夹的弧相等，等弧所对的弦相等．
练习册系列答案
相关题目
17．完成下列表格（x1，x2是方程的两根）：
结合该题，写出一元二次方程ax2+bx+c=0（a≠0）两根x1，x2与系数的关系是：x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+6=0 | 2 | 3 | 5 | 6 |
| 2x2-3x+1=0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | $\frac{1}{2}$ |
| 5x2-7x+2=0 | $\frac{2}{5}$ | 1 | $\frac{7}{5}$ | $\frac{2}{5}$ |
11．已知方程x2+2ax+1=0有两个不相等的实根，则方程x2+2ax+1+2（a2-1）（x2+1）=0的根的情况是（ ）
| A． | 有两个不等实根 | B． | 有两个相等的实根 | ||
| C． | 没有实根 | D． | 只有一个实根 |
15．下列命题中，错误的命题是（ ）
| A． | 如果两个三角形全等，那么它们的高对应相等 | |
| B． | 如果两个三角形全等，那么它们的中线对应相等 | |
| C． | 如果两个三角形的对应角平分线相等，那么这两个三角形全等 | |
| D． | 有斜边和一个锐角对应相等的两个直角三角形全等． |