题目内容
1.已知a<b<0,x=|a|,y=|b|,z=$\frac{|a+b|}{2}$,w=$\sqrt{ab}$,比较x,y,z,w的大小.分析 利用特殊值法解答即可.
解答 解:∵a<b<0,
∴令a=-4,b=-1.
∴x=|a|=|-4|=4,y=|b|=|-1|=1,z=$\frac{|a+b|}{2}$=$|\frac{-4+(-1)}{2}|$=2.5.W=$\sqrt{ab}$=$\sqrt{4}$=2.
∵1<2<2.5<4,
∴y<W<z<x.
点评 本题主要考查的是比较实数大小,特殊值法的应用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
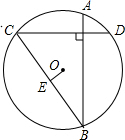 如图所示,已知⊙O弦AB⊥CD,OE⊥BC于点E,求证:AD=2OE.
如图所示,已知⊙O弦AB⊥CD,OE⊥BC于点E,求证:AD=2OE.