题目内容
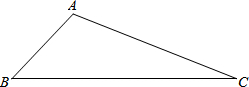
 如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.(1)求证:MN⊥DE;
(2)若BC=20,DE=12,求△DME的面积.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质,勾股定理
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得EM=DM=
BC,再根据等腰三角形三线合一的性质证明即可;
(2)求出EM,EN,再利用勾股定理列式求出MN,然后根据三角形的面积公式列式计算即可得解.
| 1 |
| 2 |
(2)求出EM,EN,再利用勾股定理列式求出MN,然后根据三角形的面积公式列式计算即可得解.
解答:(1)证明:∵CD、BE分别是AB、AC边上的高,M是线段BC的中点,
∴EM=DM=
BC,
∵N是线段DE的中点,
∴MN⊥DE;
(2)解:∵BC=20,DE=12,
∴EM=
×20=10,
EN=
DE=
×12=6,
在Rt△EMN中,MN=
=
=8,
所以,△DME的面积=
×12×8=48.
∴EM=DM=
| 1 |
| 2 |
∵N是线段DE的中点,
∴MN⊥DE;
(2)解:∵BC=20,DE=12,
∴EM=
| 1 |
| 2 |
EN=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△EMN中,MN=
| EM2-EN2 |
| 102-62 |
所以,△DME的面积=
| 1 |
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理的应用,熟记性质并准确识图是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=
如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=
 如图,在△ABC中,∠BAC是钝角,完成下列画图.(不写作法保留作图痕迹)
如图,在△ABC中,∠BAC是钝角,完成下列画图.(不写作法保留作图痕迹)