题目内容
14.计算(1)$\sqrt{32}$-$\sqrt{18}$+$\sqrt{\frac{1}{2}}$.
(2)($\sqrt{48}$-$\sqrt{27}$)÷$\sqrt{3}$.
分析 (1)首先化简二次根式,进而得出答案;
(2)首先化简二次根式,进而利用二次根式除法运算法则求出答案.
解答 解:(1)原式=4$\sqrt{2}$-3$\sqrt{2}$+$\frac{\sqrt{2}}{2}$,
=$\sqrt{2}$+$\frac{\sqrt{2}}{2}$
=$\frac{3}{2}$$\sqrt{2}$;
(2)原式=(4$\sqrt{3}$-3$\sqrt{3}$)÷$\sqrt{3}$,
=$\sqrt{3}$÷$\sqrt{3}$
=1.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4.计算(-a+2b)2-(-a-2b)2的结果是( )
| A. | -8ab | B. | -4ab | C. | 8ab | D. | 4ab |
2.如果∠A和∠B的两边分别平行,∠A=60°,那么∠B是( )
| A. | 60° | B. | 30°或120° | C. | 120° | D. | 60°或120° |
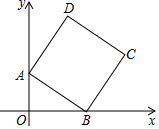 在平面直角坐标系中,O为坐标原点,直线AB与y轴交于A(0,4),与x轴交于点B.
在平面直角坐标系中,O为坐标原点,直线AB与y轴交于A(0,4),与x轴交于点B.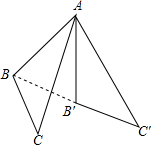 △ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.
△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.