题目内容
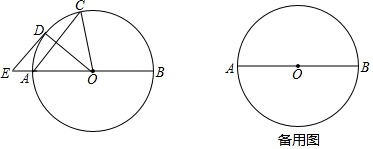
3.如图,AB是⊙O的直径,点C是半圆上的一个动点,OD平分∠AOC交⊙O于点D,过点D作DE∥AC交BA的延长线于点E.(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的直径AB=4,∠AOC=120°,请在备用图上画出符合条件的图形,并求四边形ACDE的周长.
分析 (1)根据OD平分∠AOC可得弧AD=弧CD,利用垂径定理的推论可得OD⊥AC,则DE⊥AC,然后利用切线的判定定理证得DE与圆相切;
(2)证明△COD是等边三角形,则易证四边形ACDE是平行四边形,在Rt△AOM中,根据AC=2AM即可求解.
解答 解:(1)直线DE与⊙O相切.
理由:∵OD平分∠AOC,
∴∠AOD=∠COD,
∴弧AD=弧CD,
∴OD⊥AC.
∵DE∥AC,
∴OD⊥DE,
∴DE是⊙O的切线,即直线DE与⊙O相切.
(2)如图所示,
∵OD平分∠AOC,∠AOC=120°,
∴∠AOD=∠COD=60°,
∵OA=OD,
∴△COD是等边三角形,
∴CD=OC=2,∠CDO=60°=∠AOD,
∴CD∥BE,
∵DE∥AC,
∴四边形ACDE是平行四边形,
∴AE=CD=2,DE=AC,
在Rt△AOM中,∵sin60°=$\frac{AM}{OA}$,
∴AM=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,由垂径定理得AC=2AM=2$\sqrt{3}$,
∴四边形ACDE的周长是2(2+2$\sqrt{3}$)=4+4$\sqrt{3}$.
点评 本题考查了垂径定理以及平行四边形的判定与性质,求弦长的问题转化为直角三角形的计算是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.将一枚质地均匀的硬币先后抛掷两次,则至少出现一次正面向上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
17.将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
| A. | y=2x-5 | B. | y=2x+5 | C. | y=2x+8 | D. | y=2x-8 |
15. 如图,若l1∥l2,则∠α等于( )
如图,若l1∥l2,则∠α等于( )
 如图,若l1∥l2,则∠α等于( )
如图,若l1∥l2,则∠α等于( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |

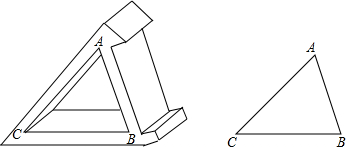
 如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39.
如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39.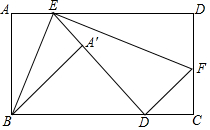 如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.
如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.