题目内容
如图,▱ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=2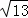 ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
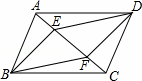
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAF=∠BCE.
又∵BE∥DF,
∴∠BEC=∠DFA.
在△BEC与△DFA中,
 ,
,
∴△BEC≌△DFA(AAS),
∴BE=DF.
又∵BE∥DF,
∴四边形BEDF为平行四边形;
(2)连接BD,BD与AC相交于点O,如图:

∵AB⊥AC,AB=4,BC=2 ,
,
∴AC=6,
∴AO=3,
∴Rt△BAO中,BO=5,
∵四边形BEDF是矩形,
∴OE=OB=5,
∴点E在OA的延长线上,且AE=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
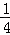 x2﹣
x2﹣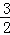 x+2与x轴交于A,B两点(OA<OB),与y轴交于点C.
x+2与x轴交于A,B两点(OA<OB),与y轴交于点C.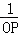 +
+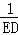 的值最小,求出这个最小值并写出此时点E,P的坐标;
的值最小,求出这个最小值并写出此时点E,P的坐标;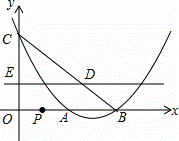
 的值是
的值是 B. 2 C.
B. 2 C.  D.
D. 

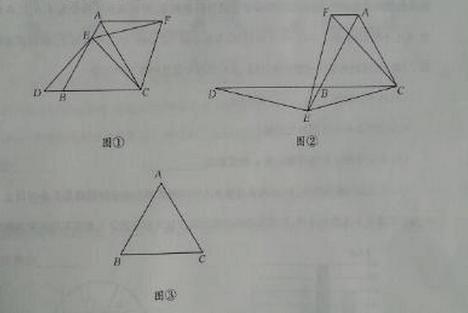
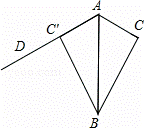
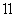 ,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转
,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转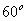 至⊿ACF,连接EF。
至⊿ACF,连接EF。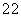 ,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。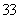 的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。
的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。