题目内容
【问题提出】
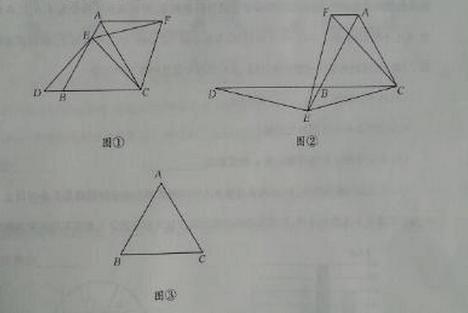
如图 ,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转
,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转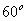 至⊿ACF,连接EF。
至⊿ACF,连接EF。
试证明:AB=DB+AF。
【类比探究】
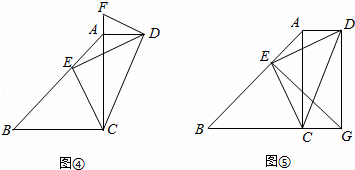
(1)如图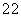 ,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
(2)如果点E在线段BA的延长线上,其他条件不变,请在图 的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。
的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。
 |
第一问是个明显的旋转问题,根据旋转的特点,我们能够得出CE=CF,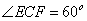 ,即
,即 是等边三角形;
是等边三角形;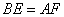 ;
;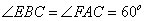 ,进而:
,进而: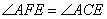 ,再有
,再有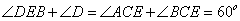
又由已知DE=CE,知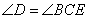 ,所以有
,所以有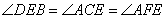 ,这样就能得出
,这样就能得出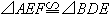
则有AE=BD,所以AB=AE+BE=BD+AF。第(2)问,根据第一问的做法,我们应该像第(1)问那样去证明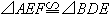 ,全等的条件都是有AF=BE(旋转得出),DE=EF,这样关键就在于说明
,全等的条件都是有AF=BE(旋转得出),DE=EF,这样关键就在于说明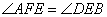 。要想说明这两个角相等,我们可以像第(1)问一样去证出
。要想说明这两个角相等,我们可以像第(1)问一样去证出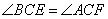 ,
,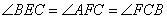 ,这样我们就能得出AF∥CD,此时我们需要把BD和EF的交点标示为G点,这样就有
,这样我们就能得出AF∥CD,此时我们需要把BD和EF的交点标示为G点,这样就有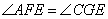 ,接下来我们可以想办法证明
,接下来我们可以想办法证明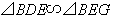 (条件有一个公用角和小角),这样就得出了
(条件有一个公用角和小角),这样就得出了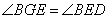 ,所以就有
,所以就有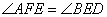 ,也就得出了三角形全等,这样就有AE=BD,所以这时AB=AE-BE=BD-AF。第(3)问画图略过,理由可以参考第(2)问。
,也就得出了三角形全等,这样就有AE=BD,所以这时AB=AE-BE=BD-AF。第(3)问画图略过,理由可以参考第(2)问。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
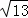 ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.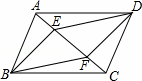
 如图,
如图,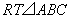 ,
,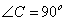 ,
,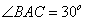 ,AB=8,以
,AB=8,以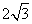 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合。现将正方形DEFG沿A→B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与⊿ABC的重合部分的面积
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合。现将正方形DEFG沿A→B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与⊿ABC的重合部分的面积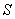 与运动时间
与运动时间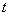 之间的函数关系图像大致是( )
之间的函数关系图像大致是( )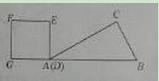
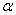 的度数是____________;
的度数是____________;
 的值为0.
的值为0. 为 cm.
为 cm.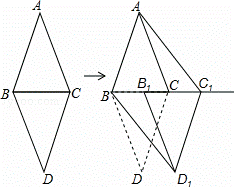
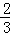 ,AD=1,求DG的长.
,AD=1,求DG的长.