题目内容
如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.
(1)求证:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)
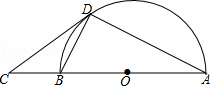
证明:(1)连接OD,如图,

∵CD与半圆O相切于点D,
∴OD⊥CD,
∴∠CDO=90°,即∠CDB+∠BDO=90°,
∵AB是半圆O的直径,
∴∠ADB=90°,即∠ADO+∠BDO=90°,
∴∠CDB=∠ODA,
∵OD=OA,
∴∠ODA=∠BAD,
∴∠BAD=∠BDC;
(2)∵∠BAD=∠BDC=28°,在Rt△ABD中,sin∠BAD= ,
,
∴AB= ,
,
∴⊙O的半径为 .
.

练习册系列答案
相关题目

 m B.
m B.  m C.
m C.  m D. 1m
m D. 1m .
. B.
B. C.
C.  D.
D. 

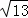 ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.