题目内容
2.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.①填空:当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为a+b(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

分析 (1)根据点A为线段BC外一动点,且BC=a,AB=b,可得当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b;
(2)①根据等边三角形ABD和等边三角形ACE,可得△CAD≌△EAB(SAS),根据全等三角形的性质可得CD=BE;
②根据全等三角形的性质可得,线段BE长的最大值=线段CD长的最大值,而当线段CD的长取得最大值时,点D在CB的延长线上,此时CD=3+1=4,可得BE=4.
解答  解:(1)如图1,∵点A为线段BC外一动点,且BC=a,AB=b,
解:(1)如图1,∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.
故答案为:CB的延长线上,a+b;
(2)①CD=BE.
理由:如图2,∵等边三角形ABD和等边三角形ACE,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD和△EAB中,
$\left\{\begin{array}{l}{AD=AB}\\{∠CAD=∠EAB}\\{AC=AE}\end{array}\right.$,
∴△CAD≌△EAB(SAS),
∴CD=BE;
②线段BE长的最大值为4.
理由:∵线段BE长的最大值=线段CD长的最大值,
∴当线段CD的长取得最大值时,点D在CB的延长线上,
此时CD=3+1=4,
∴BE=4.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,等边三角形的性质的综合应用,解决问题的关键是掌握等边三角形的性质以及全等三角形的性质.解题时注意:两边及其夹角分别对应相等的两个三角形全等.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.如果a2=(-3)2,那么a等于( )
| A. | 3 | B. | -3 | C. | 9 | D. | ±3 |
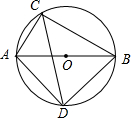 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.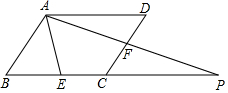 在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.
在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P. 如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),点B的坐标为(3,1),如果要使△ABD与△ABC全等.
如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),点B的坐标为(3,1),如果要使△ABD与△ABC全等.