题目内容
12.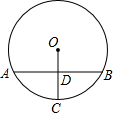 如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.
如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2$\sqrt{3}$,点E在⊙O上,∠EOA=30°,则△EOC的面积为1或2.
分析 设⊙O的半径为x(x>0),则OD=DC=$\frac{1}{2}$x,根据垂径定理可知AD=$\sqrt{3}$,在Rt△ADO中利用勾股定理即可求出x值,再分点E在$\widehat{AC}$外和点E在$\widehat{AC}$上两种情况考虑△EOC的面积,当点E在$\widehat{AC}$外时,通过角的计算可得出∠COE=90°,利用三角形的面积公式即可求出S△EOC的值;当点E在$\widehat{AC}$上时,过点E作EF⊥OC于点F,通过角的计算可得出∠COE=30°,由此可得出EF的长度,利用三角形的面积公式即可求出S△EOC的值.综上即可得出结论.
解答 解:依照题意画出图形,连接OA.
设⊙O的半径为x(x>0),则OD=DC=$\frac{1}{2}$x.
∵OC⊥AB于点D,
∴∠ADO=90°,AD=DB=$\frac{1}{2}$AB=$\sqrt{3}$.
在Rt△ADO中,AO=x,OD=$\frac{1}{2}$x,AD=$\sqrt{3}$,
∴∠OAD=30°,∠AOD=60°,AD=$\sqrt{A{O}^{2}-O{D}^{2}}$=$\frac{\sqrt{3}}{2}$x=$\sqrt{3}$,
解得:x=2.
当点E在$\widehat{AC}$外时,∠COE=∠AOD+∠EOA=90°,
∴S△EOC=$\frac{1}{2}$EO•OC=2;
当点E在$\widehat{AC}$上时,过点E作EF⊥OC于点F,
∵∠COE=∠AOD-∠EOA=30°,
∴EF=$\frac{1}{2}$OE=1,
∴S△EOC=$\frac{1}{2}$OC•EF=1.
综上可知:△EOC的面积为1或2.
故答案为:1或2.
点评 本题考查了垂径定理、勾股定理以及三角形的面积,分点E在$\widehat{AC}$外和点E在$\widehat{AC}$上两种情况考虑是解题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | x3y4与x4y3 | B. | -3xy与xz | C. | 5ab与-2ba | D. | -3x2y与$\frac{1}{2}{x^2}yz$ |
| A. | (-3)2与-32 | B. | (-3)2与32 | C. | (-2)3与23 | D. | (-2)3与|-2|3 |
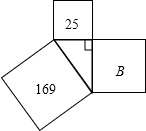 如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:
如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题: 如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)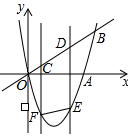 如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.
如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.