题目内容
13.“当a≠0时,a-p=$\frac{1}{{a}^{p}}$或a-p=($\frac{1}{a}$)p,例如:2-2=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,($\frac{2}{3}$)-3=($\frac{3}{2}$)3=$\frac{27}{8}$”,请计算(-$\frac{1}{2}$)-3=-8.分析 根据当a≠0时,a-p=$\frac{1}{{a}^{p}}$或a-p=($\frac{1}{a}$)p,可得答案.
解答 解:(-$\frac{1}{2}$)-3=(-2)3=-8,
故答案为:-8.
点评 本题考查了负整数指数幂,利用了当a≠0时,a-p=$\frac{1}{{a}^{p}}$或a-p=($\frac{1}{a}$)p.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.解方程$\frac{2x+1}{3}$-$\frac{10-x}{6}$=1时,去分母正确的是( )
| A. | 2x+1-10-x=1 | B. | 4x+2-10+x=1 | C. | 4x+2-10-x=6 | D. | 4x+2-10+x=6 |
5.若分式$\frac{2+x}{{x}^{2}-4}$有意义,则x的取值范围是( )
| A. | x≠2 | B. | x≠±2 | C. | x≠-2 | D. | x≥-2 |
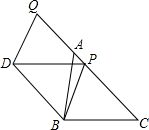 如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.
如图,在△ABC中,AB=8,sin∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为6.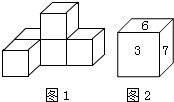 (1)画出下图1中几何体的三视图.
(1)画出下图1中几何体的三视图.