若分式$\frac{2+x}{{x}^{2}-4}$有意义.则x的取值范围是( )A．x≠2B．x≠±2C．x≠-2D．x≥-2 题目和参考答案——青夏教育精英家教网——

题目内容

5．若分式$\frac{2+x}{{x}^{2}-4}$有意义，则x的取值范围是（　　）

A．

x≠2

B．

x≠±2

C．

x≠-2

D．

x≥-2

分析利用分是有意义的条件进而求出即可．

解答解：∵分式$\frac{2+x}{{x}^{2}-4}$有意义，
∴x²-4≠0，
解得：x≠±2，
则x的取值范围是：x≠±2．
故选：B．

点评此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．

练习册系列答案

胜卷在握系列答案

优化学案系列答案

体验型学案系列答案

周周大考卷系列答案

激活思维优加课堂系列答案

全能达标100分系列答案

智能考核卷系列答案

活力试卷系列答案

琢玉计划系列答案

小学全能测试卷系列答案

相关题目

7．x取什么值时，下列各式在实数范围内有意义？
（1）$\sqrt{x-4}$；
（2）$\sqrt{1+{x}^{2}}$；
（3）$\sqrt{4-6x}$；
（4）$\frac{1}{\sqrt{2-3x}}$．

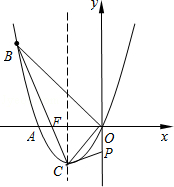如图，已知抛物线经过A（-2，0），B（-3，3）及原点O，顶点为C．
（1）求抛物线的函数解析式．
（2）设点D在抛物线上，点E在抛物线的对称轴上，若四边形AODE是平行四边形，求点D的坐标．
（3）联接BC交x轴于点F．y轴上是否存在点P，使得△POC与△BOF相似？若存在，求出点P的坐标；若不存在，请说明理由．

13．“当a≠0时，a^-p=$\frac{1}{{a}^{p}}$或a^-p=（$\frac{1}{a}$）^p，例如：2^-2=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$，（$\frac{2}{3}$）^-3=（$\frac{3}{2}$）³=$\frac{27}{8}$”，请计算（-$\frac{1}{2}$）^-3=-8．

20．一个长方形的周长是30cm，若长方形的一边长为a cm，用代数式表示该长方形的面积是（15a-a²）cm²．

10．已知a、b为两个连续的整数，且a＜$\sqrt{39}$＜b，则a+b=13．

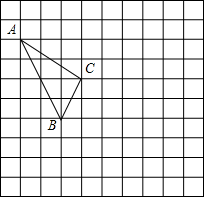已知△ABC的顶点A（-4，5），B（-2，1），完成下列问题：
（1）在如图所示的网格中建立直角坐标系；
（2）作出△ABC关于y轴对称的△A′B′C′；
（3）写出点C′的坐标．

14．小明和小亮是上海某高校的大学生，他们参加世博志愿者选拔并与甲、乙二人都进入了前4名．现从这4名入选者中确定2名作为志愿者．试用画树形图或列表的方法求出小明和小亮同时入选的概率．

15．当x=4时，代数式3x-5的值与$\frac{1}{7}$互为倒数．